后缀自动机与后缀树
摘要
粗略地,对字符串定义 SAM:
- 是状态集合:的等价类的集合。
- 是字符集:的字符集;
- 是转移函数:对于,表示在状态的末尾添加字符到达的状态。
- ()是初始状态:。
- ()是终止状态:的后缀所在等价类的集合。
在常见的代码实现过程中,会记录额外的信息:
- ,对于,表示的最近父类对应的状态。
等价类代表一个的子串集合,使得且:
- 要么是的后缀,要么是的后缀。
- 在中的出现次数与在中的出现次数相等。
设表示()在中出现的次数。那么我们称是的父类(包含)当:
- ,是的后缀。
- 。
也就是说等价类都包含它的父类,可以类比面向对象中的类继承。
等价类的最近父类是指它的父类中最小的那个。
后缀自动机
后缀自动机(Suffix Automaton,SAM)是一种有限状态自动机。对于一个 SAM,其转移函数是以字符集为转移条件,将当前状态转移到另一状态的函数。
这个状态分两种:合法与不合法。说白了就是存在和不存在。如果一个字符串不被 SAM 接受,那么就会转移到空指针。初始状态是根结点,也就是字符串开头。
性质
SAM 的空间复杂度与建立的时间复杂度是的。
对建立的后缀自动机包含的所有子串。因为的子串一定是其某一后缀的前缀。
不同于 AC 自动机,后缀自动机是一个 DAG。
后缀自动机中的每一个状态对应了一类子串,这一类子串长度个不相同,并且按长度排序后前一个是后一个的后缀。
等价类
我们假设这一类子串中最长的子串是,那么这一类子串满足这样的关系:的后缀在 S 中的出现的位置是相同的。这类字符串被称为等价类。
包含类
还有一种情况,就是 S 的某一子串的后缀在 S 中出现的位置比多,那么称是的包含类。为什么包含?因为出现的位置一定出现,而出现的位置不一定出现。
Fail 树
SAM 除了构建自动机还会构建一个 fail 树,fail 树中,当前状态的父结点总是它的包含类,即它的某个后缀形成的等价类。结合等价类和包含类,使得 SAM 的空间复杂度降到了线性级别。
也可以说,fail 指针指向它的最长的出现次数比它多的后缀。
模板
const int SZ=2e6+6,ALP=26;
struct SAM{
int tot,last;
int tr[SZ][ALP],len[SZ],fail[SZ];
SAM(){tot=last=1;}// 初始化
void insert(int x){
int u=++tot,p=last;// 新建结点,p 是在 fail 上跳指针用的
len[u]=len[last]+1,last=u;
while(p&&tr[p][x]==0)tr[p][x]=u,p=fail[p];// 更新 last 在 fail 树上的祖先的转移函数
// 接下来,我们求新建结点 u 的 fail 指针,同时会更新 fail 树
if(!p)fail[u]=1;// 跳到根结点的 fail
else {
int q=tr[p][x];
if(len[q]==len[p]+1)fail[u]=q;
else{
// 如果不是 0,说明结点 p 在之前就存在字符 x 的转移函数
// 那么就考虑这个转移到达的状态是否是等价类
// 如果是等价类,那么 fail 就指向 q;
// 否则就要从中分离出一个包含类,然后指向这个结点
int cq=++tot;
len[cq]=len[p]+1,fail[cq]=fail[q];
memcpy(tr[cq],tr[q],sizeof(tr[q]));
fail[u]=fail[q]=cq;
while(p&&tr[p][x]==q)tr[p][x]=cq,p=fail[p];
}
}
}
}后缀树
首先我们了解一下后缀树的概念。最基本的后缀树就是把一个串的所有后缀建一个 Trie。以 ababb 为例:
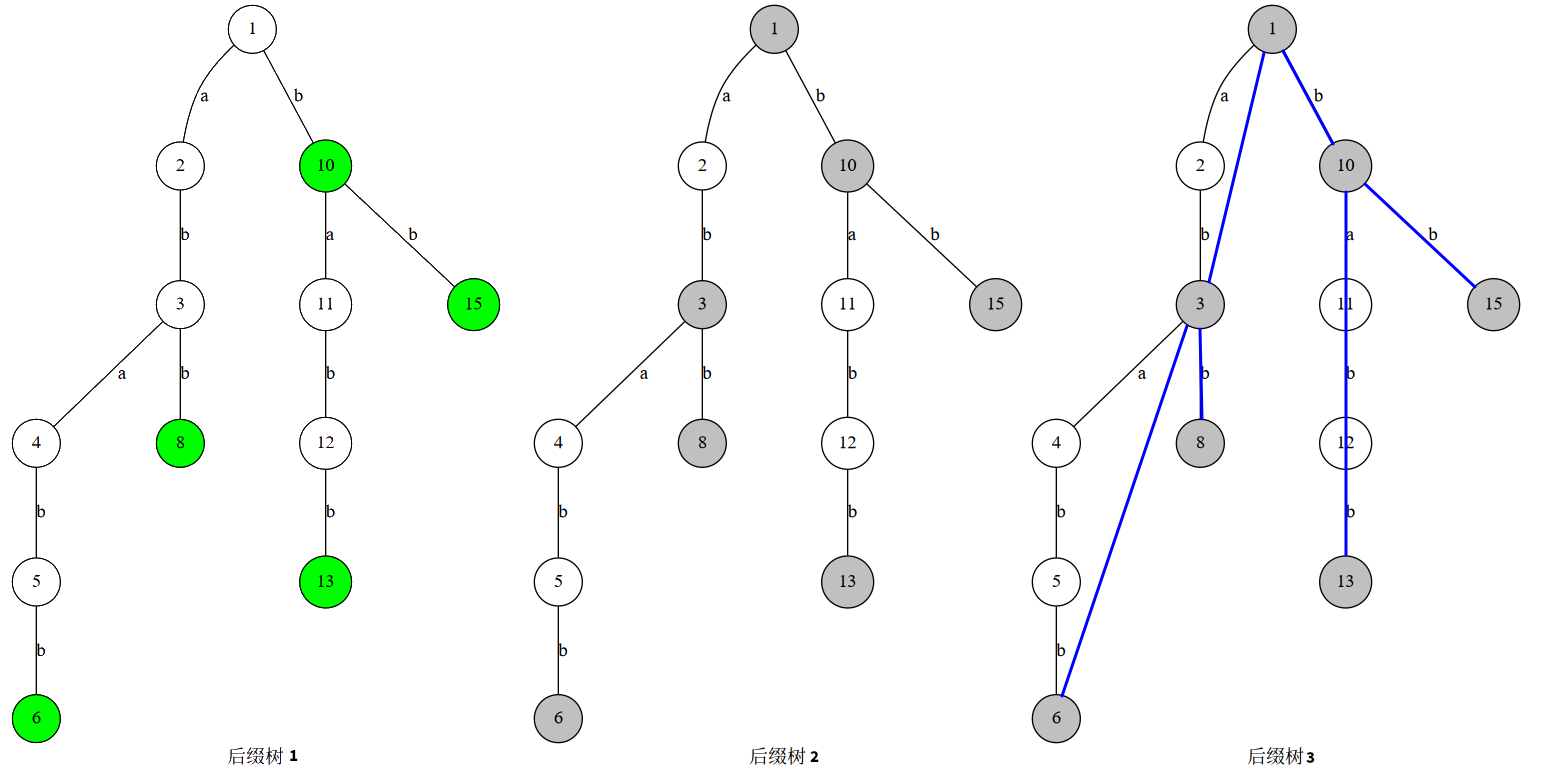
绿色的点表示接受状态的结点(即后缀的末尾)。我们将除了二度点以外的标记为关键点(因为这些点可以刻画这棵树的大致结构),如图 2。
灰色结点为关键点,并且我们认为接受状态的结点是关键点(尽管它有可能是二度点)。这个后缀树的简化后缀树相当于关键点构成的树,如图 3。
蓝色边构成的树即为简化后缀树。
理解增量构造法
后缀树与后缀自动机
一个串的 SAM 的 Fail 树是其反串的简化后缀树,反串简化后缀树的结点与 SAM 的结点一一对应。
反串后缀树上结点的深度就对应 SAM 上该状态(结点)的长度。
例如我们对 bbaba 建立后缀自动机:
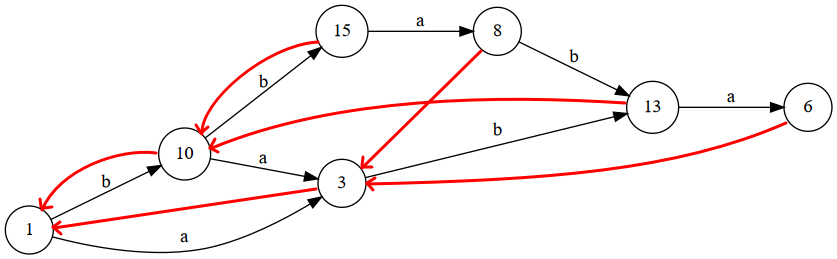
可以发现,红树和上文的蓝树是一样的!
那么为什么是这样的呢?我们感性理解一下。前文所述的 SAM 可以理解为最简状态的 SAM,它将重复的状态合并。而我们把反串的后缀树取一个最简后缀树,其实就是在做类似的事情。
事实上,反串后缀树上的一条从根挂下来的路径对应原串的一个后缀,它到达的状态就是这个路径往下走遇到的第一个关键点!
比如在后缀树的图中的 aba,abab,ababb,对应原串的 aba,baba,bbaba,把他们在 SAM 上跑一遍,都会跑到结点去。即结点在 SAM 上接受的状态是 aba,baba,bbaba。
这样,对 SAM 的操作就可以与对后缀树的操作形成对应。
类似地,可以将 SAM 的转移边对应到简化后缀树上。转移边相当于在后面添加一个字符,则在反串简化后缀树上就是在开头加一个字符,然后转移到对应状态的结点。
SAM 的构造方法是一个增量构造法。我们可以通过反串简化后缀树来理解它。
例如在 bbaba 的后面添加一个字符 b。则相当于在反串开头添加一个 b,那么我们相当于把 bababb 插入到简化后缀树上,完成的效果是这样的:
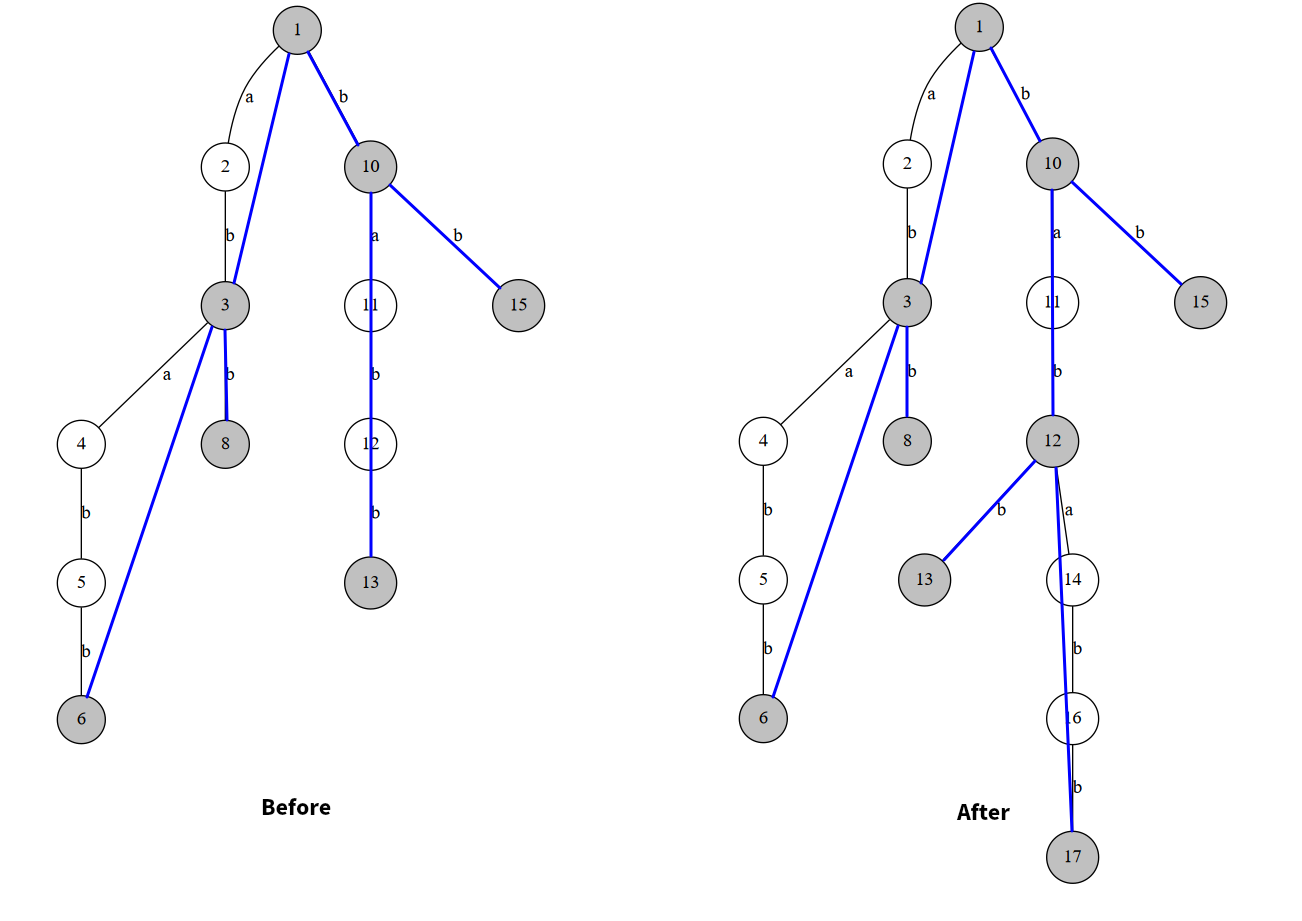
但是你无法像 Trie 一样直接插入,因为你维护 SAM 的时候是没有这么多信息的,你只知道简化后缀树的信息,即关键点。因此我们尝试用 SAM 的操作来完成这个过程。
要在增量构造 SAM 的同时增量构造反串的简化后缀树,首先考虑增加一个字符带来的影响。
设表示 SAM 中所在的等价类,即所有等价类的子类。在末尾添加一个字符,相当于新建一个状态,并给增加的转移。同时,可能有的一些父类也能转移到,因此也一并加上。
接下来我们就要确认的最近父类,设其为。
- 首先,如果的父类中不存在通过转移得到的状态,说明这个是一个新的字符。那么的父类就是()。
- 否则,可以判断,一定是由的某个父类“分裂”之后,再在其中的每个字符串末位加上得到的。分裂的原因是,在末尾加入了之后,中的某些字符串的出现次数发生了变化,而某些又保存不变。
还有一件事情。在第一步的过程中我们把以及的父类对字符建立了向的转移。而如果遇到本身存在的情况,意味着我们找到了用于构造父类的等价类。这时我们会直接进行第二步的过程。第二步的过程会给中途插入一个分裂出的父类。因此所有的,关于字符的,原本指向的转移,都得改为指向。因此我们要把的父类都做更新。
这样就完成了增量的过程。
一个具体示例
第一部分
首先,SAM 的指针指向结点。反串后缀树上结点对应路径表示的就是它接收的最长的那个状态(SAM 上的结点接受aba,baba,bbaba三个状态,而bbaba是最长的,对于反串后缀树上的路径是 ababb)。
而你在这个状态开头添加一个 b,相当于在 SAM 上通过转移边()跳转到对应状态。而是没有的,因此我们要跳到在简化后缀树上的父节点。因为这个父节点的状态是的状态的后缀(别忘了是反串),而跳父节点就相当于是 SAM 上跳指针。
于是我们这样不断跳指针直到有一个结点的存在,在这个例子中,3 结点存在。则我们转移到,在简化后缀树中 13 包含了的状态(12 的状态即为bab,指反串)。
现在相当于,我们要把插入到简化后缀树中,然后从分叉,连出去一条链把剩下的状态补齐(即bababb-bab=abb)。
把加入到简化后缀树,则需要更新的简化后缀树上的父节点指针(对应 SAM 的 fail 指针)。
然后从连出去一条链,在简化后缀树上就是一条边(可以理解边权为 abb),然后连出这个新的结点也要更新它的简化后缀树上的父节点指针(SAM 上 fail 指针)。
第二部分
最后有一件简化后缀树考虑不完全的事情,就是对转移函数的更新()。因为转移函数并不能直观地在反串简化后缀树上表现。但我们仍可以这么理解。
重新回到一开始。在我们不断跳 fail 寻找是否存在的时候,如果这个结点不存在,可以将它事先指向我们新建的代表(原串状态为bbabab)的结点。事实上你也应该这么做,这样才能保证转移函数的完整性。
第三部分
由于结点本来转移到(),现在我们加了一个结点,那么自然(其实结点本来就转移到,但是在之前的 SAM 中状态是被归在结点上的。现在相当于我们把这个状态分离出来)。既然是存在的,而在简化后缀树上的祖先结点状态又是它的后缀状态,因此也存在字符 b 的转移边,那么显然要一并改成。于是我们就需要在的基础上不断跳并更新字符b的转移函数。
修订记录
- 2020年7月23日 创建文章