连通分量相关算法

有向图 DFS 生成树

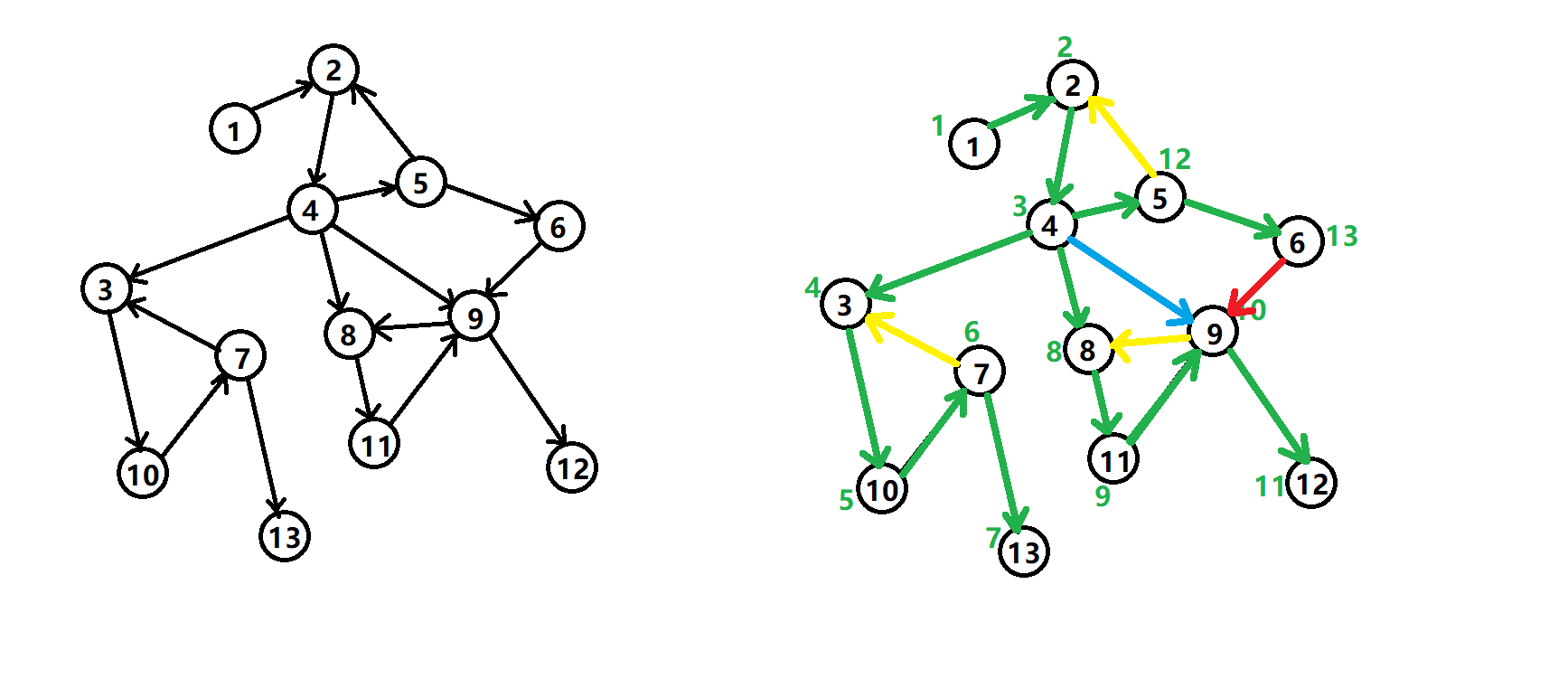
有向图的搜索树主要有$4$种边（不一定全部出现）：

1. 树边（tree edge）：绿色边，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
2. 反祖边（back edge）：黄色边，也被叫做回边，即指向祖先结点的边。
3. 横叉边（cross edge）：红色边，它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前结点的祖先时形成的。
4. 前向边（forward edge）：蓝色边，它是在搜索的时候遇到子树中的结点的时候形成的。

强连通分量

强连通图：对于有向图$G=(V,E)$，如果对于任意结点$u,v$，存在一条$u$到$v$的有向简单路径，也存在一条$v$到$u$的有向简单路径，则称$G$是强连通图。

强连通分量：另外，对于有向图$G$点集$V$的一个子集$V'$，如果$G$关于$V'$的导出子图$G[V']$是强连通图，则称$G[V']$是$G$的强连通分量。

我们考虑 DFS 生成树与强连通分量之间的关系。

如果结点$u$是某个强连通分量在 DFS 树中遇到的第一个结点（这通常被称为这个强连通分量的根），那么这个强连通分量的其余结点一定在 DFS 树中以$u$为根的子树中。

证明：反证法。假设有个结点$v$在该强连通分量中但是不在以$u$为根的子树中，那么$u$到$v$的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边，然而这两条边都要求指向的结点已经被访问过了，这就和$u$是第一个访问的结点矛盾了。

Tarjan 算法：

TARJAN(int u,int k)
    vis[u]=true
    low[u]=dfn[u]=k
    将 u 圧入栈中
    for 与 u 相邻的结点 v
        if 结点 v 未被访问过
            TARJAN(v,k+1)// 搜索
            low[u]=min(low[u],low[v])// 回溯
        else if v 在栈中
            low[u]=min(low[u],dfn[v])
    if low[u] = dfn[u]
    	则将栈中 u 以及 u 之上的结点全部弹出
    	这些结点构成一个强连通分量

无向图 DFS 生成树

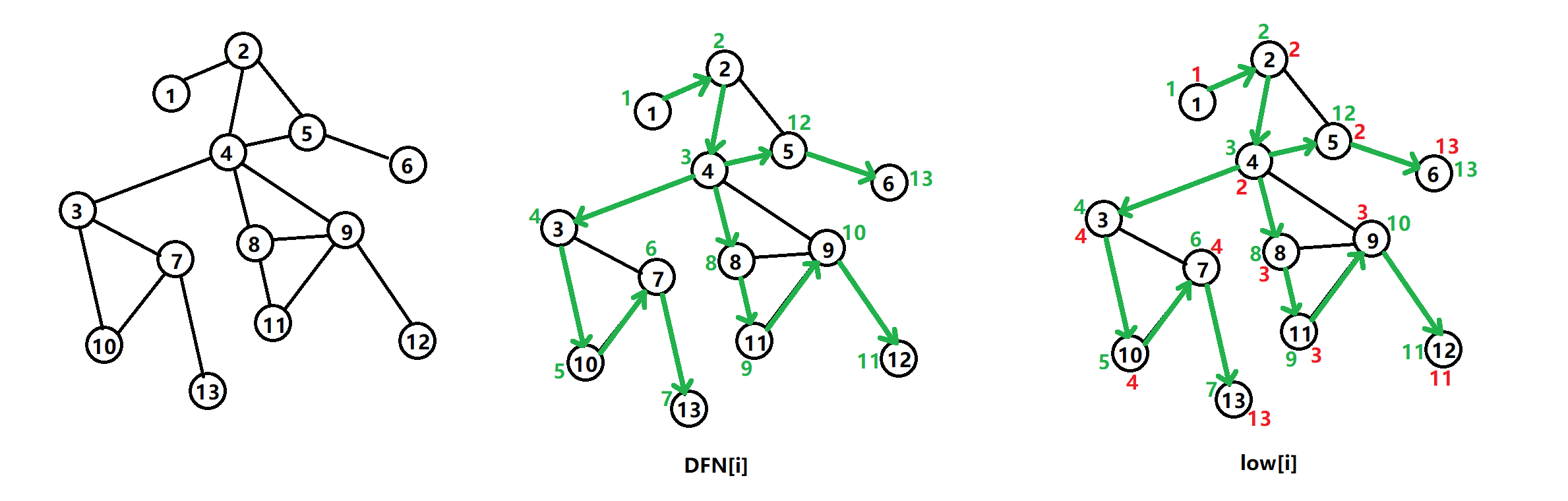
DFS 生成树：即对图进行 DFS 遍历时所有递归到的边组成的树。

设以$x$为根的子树为$T_x$。

$\text{low}(x)$定义为以下结点的 DFN 的最小值（与 Tarjan 有向图中的$\text{low}(x)$区分）：

1. $T_x$中的结点；
2. 通过一条不在搜索树上的边能到达$T_x$的结点。

不难发现，$\text{low}(x)$按 DFS 生成树的递归遍历顺序是单调递增的，因此可以在回溯的过程中求出$\text{low}(x)$。

无向图的割点与割边

割点：对于无向图$G=(V,E)$中的结点$u$，如果删掉它以及与它相连的边后，整个图连通块数量增加，则结点$u$被称为无向图的割点。

割边：对于无向图$G=(V,E)$中的边$(x,y)$，如果删掉它后，整个图连通块数量增加，则$(x,y)$被称为无向图的割边，也称作桥。

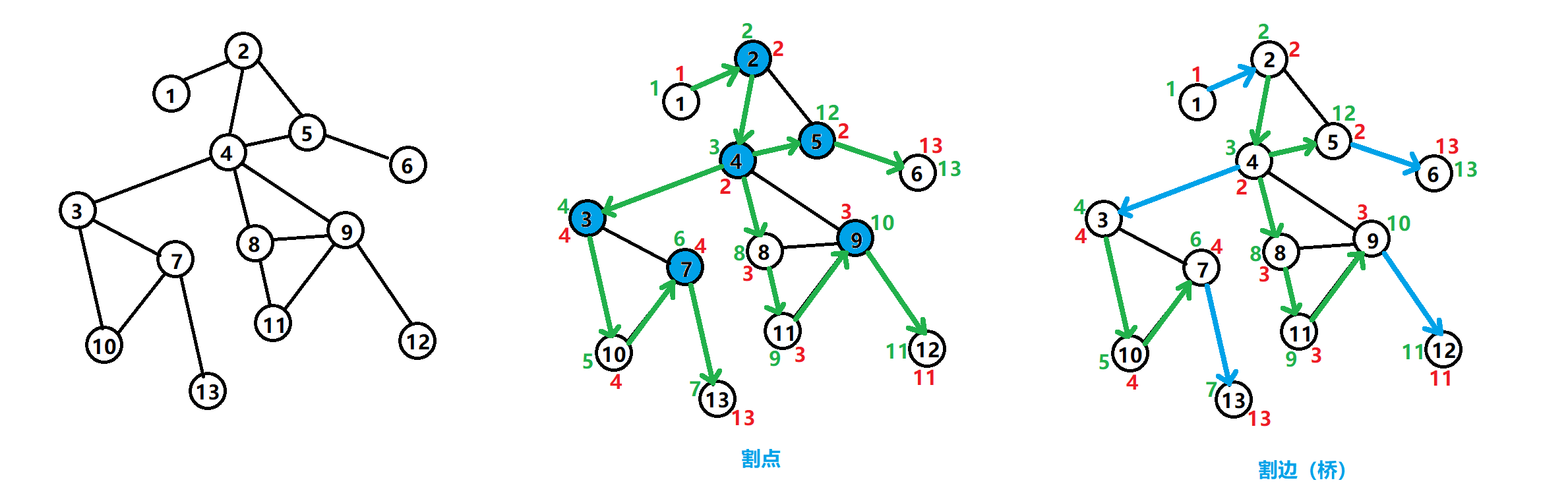
判定割边

判定割边$(x,y)$的条件：

1. $(x,y)$是 DFS 树上的边。
2. 令$x$是$y$的父结点，则满足$\text{DFN}(x)<\text{low}(y)$。也就是说，从$T_x$出发，不经过$(x,y)$的前提下无法走到更早访问的结点，则$(x,y)$作为$T_x$与图$G[V\setminus T_x]$的唯一连接，即为割边。

int dfn[N],low[N],dfn_cnt;
int ans[N],cnt;
void tarjan(int k,int p){ //tarjan 找桥，根结点的父节点为 0
	dfn[k]=low[k]=++dfn_cnt;
	for(int i=h[k]; i; i=e[i].nex){
        int u=e[i].t;
		if(!dfn[u]){
            tarjan(u,k);
			low[k]=min(low[k],low[u]);
			if(dfn[k]<low[u])ans[++cnt]=e[i].idx;// 桥
		} else if(u!=p) low[k]=min(low[k],dfn[u]);
	}
}

判定割点

判定割点$x$的条件：

1. 若$x$不为根结点，则要求，存在$x$的子结点$y$，满足$\text{DFN}(x)\leq \text{low}(y)$。 即$T_y$中的结点最多能走到结点$x$，那么将$x$删除就会导致$T_y$不连通。
2. 若$x$是根结点，则要求存在至少 2 个的子结点$y$，满足$\text{DFN}(x)\leq \text{low}(y)$。

int dfn[N],low[N],totdfn;
bool cut[N];
int ans[N],la;
void tarjan(int u,int p){
    dfn[u]=low[u]=++totdfn;
    int cnt=0;
    for(int i=h[u];i;i=e[i].nex){
        const int v=e[i].t;
        if(!dfn[v]){
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            cnt+=dfn[u]<=low[v];
        }else low[u]=min(low[u],dfn[v]);
    }
    if(cnt-(p==0)>=1)cut[u]=1;
}

无向图的双连通分量

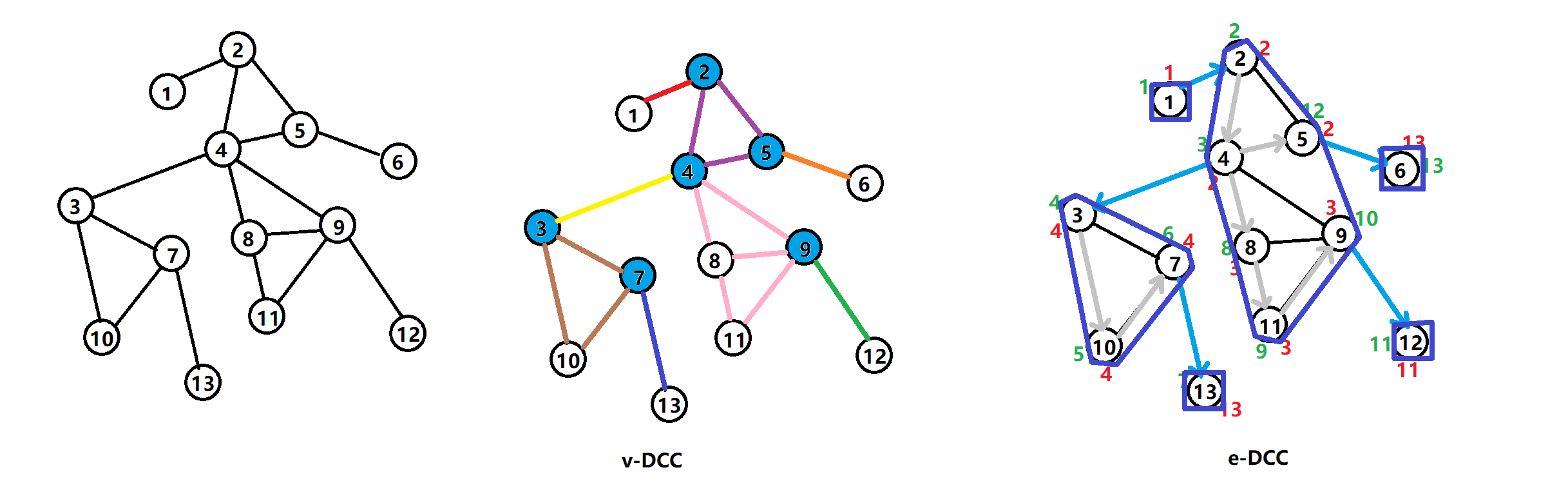
边双连通分量

对于无向图$G=(V,E)$，若其子图$G'$内不存在割边，则称$G'$是$G$的边双连通分量。

对于图$G$，直接删掉所有割边，剩下分量的就是边双连通分量。

将边双连通分量缩点，就得到了$G$的边双树。

点双连通分量

无向图$G$的子图$G'$内不存在割点，则称$G'$是图$G$的点双连通分量。

对于图$G$，割点可能同时属于多个点双连通分量，但每一条边一定只属于一个点双连通分量。

图中通过边的不同颜色来标记点双连通分量。

求点双连通分量，需在 Tarjan 算法中维护一个栈：

• 当结点$x$被第一次访问时，把该结点入栈。
• 当割点判定条件$\text{DFN}[x]\leq \text{low}[y]$成立时，无论$x$是否为根：
  • 从栈顶不断弹出结点，直到$y$被弹出。
  • 刚才弹出的所有结点与结点$x$一起构成一个点双连通分量。

点双连通分量与圆方树有密切联系。