小技巧
差比数列
不知为什么想要补一下这个。
一个等差数列,等比数列,则差比数列.
差别数列求和,使用裂项法,公式为
拉格朗日插值
2019.6.29
对于一个 n 次多项式,可以由 n+1 个点唯一确定:.
现在我们想要求这个表达式在某个位置的值。
构造一个多项式
它被成为拉格朗日基本多项式。也称插值基函数。这个表达式有什么特点?
于是可以构造这样一个多项式
它显然经过了。于是代入一个点即可得到对应位置上的值。
化简后可以得到这个多项式的系数表示法。
取值连续
我们考虑一种特殊的情况,当时,我们得到
其中。于是得到的多项式为
预处理可以求。
欧拉回路
欧拉回路指一个图中经过所有边的回路。分有向图欧拉回路和无向图欧拉回路两种。求欧拉回路可以直接采用 DFS 的方法。我们首先沿着路径不停地搜索,途中可能会掠过一些环,但我们不担心。因为我们是在回溯的时候记录路径,而回溯的时候会遍历这些没有走过的环。因此不会走漏。在搜索时可以更改前向星的头指针来剪枝。对于无向图的情况,需要记录每一条无向边(一条无向边在存的时候相当于两条有向边)是否访问过。
UOJ117
#include<algorithm>/*{{{*/
#include<cctype>
#include<cassert>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<ctime>
#include<iostream>
#include<map>
#include<queue>
#include<set>
#include<vector>
using namespace std;
typedef long long lld;
typedef long double lf;
typedef unsigned long long uld;
typedef pair<int,int> pii;
#define fi first
#define se second
#define pb push_back
#define mk make_pair
#define FOR(i,a,b) for(int i=(a);i<=(b);++i)
#define ROF(i,a,b) for(int i=(a);i>=(b);--i)/*}}}*/
/******************heading******************/
const int M=1e6+5,N=1e6+5;
int t,n,m;
int a[M],la;
struct qxx{int nex,t,v;};
qxx e[M];
int h[N],le;
void add_path(int f,int t,int v){e[++le]=(qxx){h[f],t,v},h[f]=le;}
bool vis[N];
int d1[N],d2[N];
void dfs(int u){
for(int i=h[u];i;i=h[u]){
while(i&&vis[e[i].v])i=e[i].nex;
h[u]=i;
const int v=e[i].t,w=e[i].v;
if(i)vis[w]=1,dfs(v),a[++la]=i%2?w:(t==2?w:-w);
}
}
int main(){
scanf("%d%d%d",&t,&n,&m);
int u1,v1;
FOR(i,1,m){
scanf("%d%d",&u1,&v1);
add_path(u1,v1,i);
if(t==1)add_path(v1,u1,i);
d1[u1]++,d2[v1]++;
}
FOR(i,1,n)if((d1[i]&1)^(d2[i]&1)||(t==2&&d1[i]!=d2[i]))return puts("NO"),0;
dfs(u1);
if(la<m)return puts("NO"),0;
puts("YES");
ROF(i,la,1)printf("%d ",a[i]);
return 0;
}欧拉回路有一些经典的应用
对于一个无向图,将其中的每一条边定向,要求每个结点的入度和出度的差不超过 1。
首先找到图中所有的奇点,将他们连向一个虚点 s。由于奇点的个数一定是偶数个,因此连完后整个图是欧拉图,跑一遍欧拉回路可以定向。然后再删掉 s 以及连接 s 的边,点的度最多变化 1。
平面上 n 个整点,要求将他们染成红色或者蓝色,且每行每列红蓝点个数差不超过 1。
把当作之间连一条无向边,则染红色蓝色相当与给无向边定向,转化为上一题的模型。
生成长度为的首位相接的串使得所有长度为的 01 串都出现过。
这道题其实有两种转化模型的方式。对于一个串,你可以在后面加一个 0/1 然后删除首个字符得到下一个串,因此一个串连向两个串。问题转化为寻找哈密尔顿回路问题,貌似不太可做。
另一种转化方式是,把一个形如abcd的串拆成 (abc,bcd) 的边。这样建出来的图是可能有自环的,然后我们在这个有向图上跑欧拉回路就行了。
给一个无向图(不一定连通)加边使之成为一个欧拉图。
首先处理每一个连通块。对于有奇点的连通块们显然可以连一个大环搞掉两个奇点,剩下的奇点随便匹配就行。
然后就考虑剩下若干个没有奇点的连通块,那么我们也连一个大环就行了。
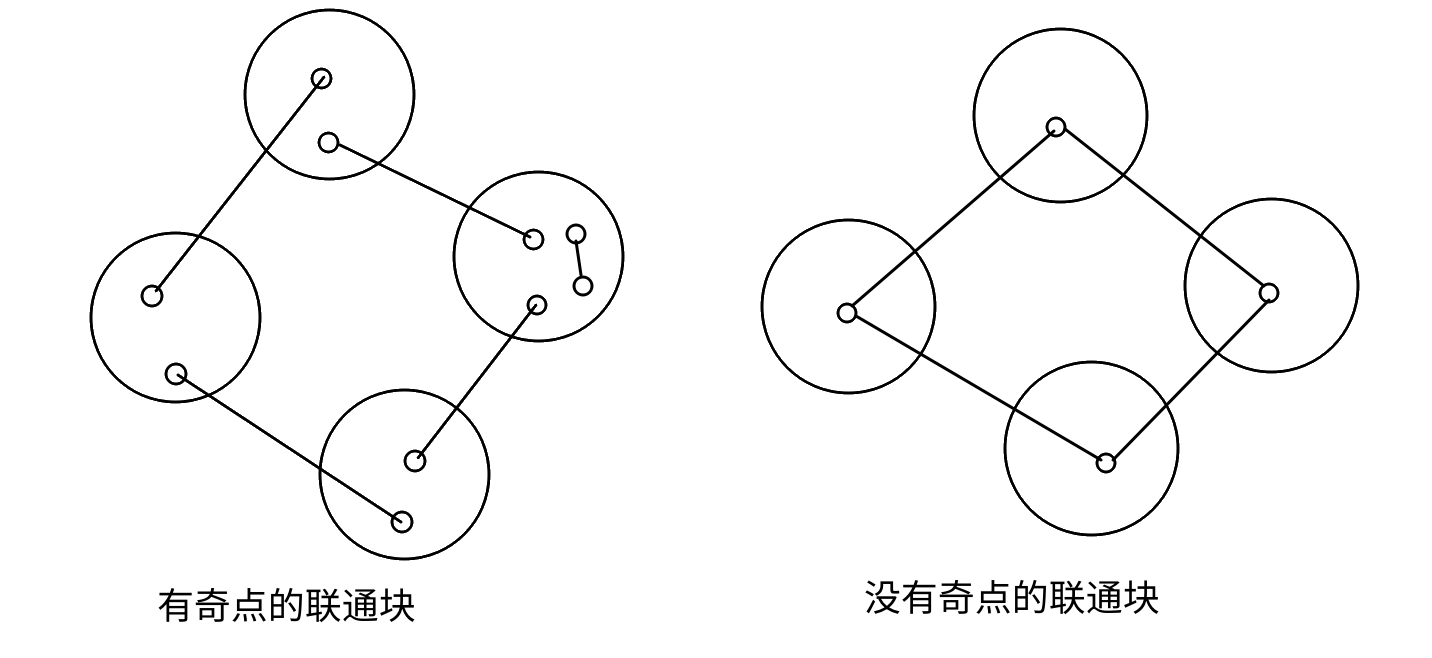
在遇到一些和欧拉回路有关的问题的时候,有时是不需要建图的,直接搞度数 ;混合图求欧拉回路需要用网络流;欧拉回路只和每个点的奇偶性有关;出一道欧拉回路的好题非常难。
DFS 及其应用
手写栈模拟 DFS:相当于把状态丢到结构体里,手动开栈,跑一个 while 循环。搜索相当于圧栈。状态不仅仅包括函数参数,还有递归结构内的一些变量的值,比如循环变量 i 的值。同时还有递归、回溯的状态之分(总之先口糊一波,以后再补)
有一些图论构造题,可以在一棵 DFS 生成树上构造而忽略非树边。这常用在证明中,也有显示的构造。
一个无向图的 DFS 生成树,每一条非树边对应一个简单环。这个可以应用在仙人掌判定上。即把每个环的结点做标记,最后判断每条树边是否只覆盖一次。
连通分量的应用
强连通分量容易让人想到缩点 DP;边双连通分量缩点后构成一棵树,称作边双树;对于点双连通分量,一个点可能在多个点双中出现。
abs 与 fabs
abs 是憨批。如果不 using namespace std 直接调用 abs 可能调用的是 int abs(int)。使用 fabs 是最保险的。
维护连续段
今天写了一个感觉很妙的 set 维护连续段的代码,感觉很简洁:
struct Interval {
int l, r, w, t; // a[l..r] = w, assigned time
bool operator<(Interval a) const { return l < a.l; }
};
set<Interval> s;
void mergeInterval(Op cur, int t) { // [cur.l, cur.r] 是我们要合并的区间
auto st = s.upper_bound({cur.l}); // 因为 l 是 struct 里第一个参数所以这里可以这么写
--st;
auto ed = s.upper_bound({cur.r});
vector<Interval> v(st, ed); // 拿出所有与之相交的区间
s.erase(st, ed);
auto & vst = v[0], & ved = v[v.size() - 1];
if(vst.l < cur.l) { // 把不在 [cur.l, cur.r] 里的区间塞回去
s.insert({vst.l, cur.l - 1, vst.w, vst.t});
vst.l = cur.l;
}
if(cur.r < ved.r) { // 把不在 [cur.l, cur.r] 里的区间塞回去
s.insert({cur.r + 1, ved.r, ved.w, ved.t});
ved.r = cur.r;
}
for(auto i : v) { // 处理被删掉的区间
if(t - 1 >= 0) qs[t - 1].push_back({i.l, i.r, 1, i.w});
if(i.t - 1 >= 0) qs[i.t - 1].push_back({i.l, i.r, -1, i.w});
}
s.insert({cur.l, cur.r, cur.w, t}); // 插入 [cur.l, cur.r]
}修订记录
- 2022年11月7日 第8次修订
- 2022年11月7日 第7次修订
- 2021年7月10日 第6次修订
- 2021年6月28日 第5次修订
- 2021年6月22日 第4次修订
- 2021年3月27日 第3次修订
- 2021年3月10日 第2次修订
- 2020年2月28日 创建文章