虚树入门

虚树

虚树是指对一棵树$T=(V,E)$，取其点集的子集$S\subseteq V$作为关键点集，将关键点以及他们两两之间的 LCA 构成的点集$S'$拿出来建立一棵树，这棵树称为$T$的关于$S$的虚树。

虚树的意义是它只包含了关键点以及 LCA，但也维护了原树的结构特征，方便我们对信息的处理。

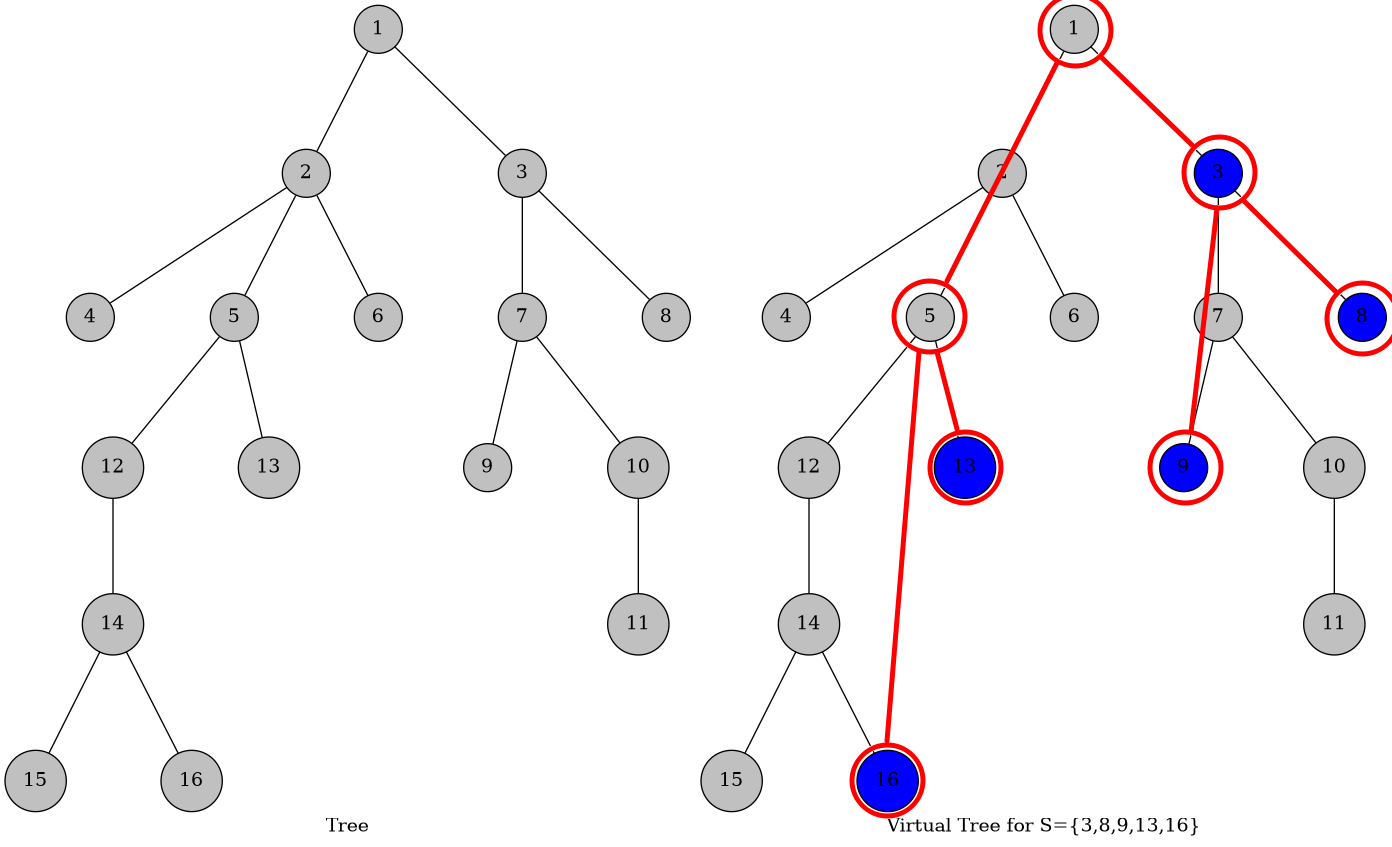
虚树的构建

我们对原树先做一次 DFS，求出每个点的 DFS 序。然后把关键点按照 DFS 序排序。考虑增量构造。我们用栈维护当前虚树的右链。添加一个结点相当于删掉末端的一些点，再把这个点加入到右链上。

在弹栈的时候就把这条边加到虚树上。最后把栈里所有的点依次连边加到虚树上即可。

int s[N],tp;
void build_virtual_tree(vector<int> & V){
    int root=V[0];
    for(int u:V)root=lca(root,u);
    s[tp=1]=root;
    for(int u:V){
        int y=lca(s[tp],u);
        while(tp>1&&dep[y]<dep[s[tp-1]])
            Vadd(s[tp-1],s[tp],W(s[tp-1],s[tp])), --tp;
        if(y==s[tp]);
        else {
            assert(tp>1);
            if(y==s[tp-1]) Vadd(y,s[tp],W(y,s[tp])), --tp;
            else Vadd(y,s[tp],W(y,s[tp])), s[tp]=y;
        }
        s[++tp]=u;
    }
    while(tp>1) Vadd(s[tp-1],s[tp],W(s[tp-1],s[tp])), --tp;
}
// s 和 tp 是栈
// V 表示关键点集，并且已经排好序。
// Vadd 表示在虚树上加上这条边，W 表示边权
// root 在特殊情况也可能是 T 的根

考虑到排序的复杂度，虚树的构建复杂度是$O(|S|\log_2|S|)$的。

小性质：虚树的规模是$\Theta(|S|)$的。

「例 1」 SDOI2011 消耗战

给出一棵边带权的树$T=(V,E)$，多次询问，每次给出一个点集$S\subseteq V$，$1\notin S$，要求删掉权值和最小的边使得 1 与$S$中任意一个点都不连通。求这个最小权值和。

$|V|\le 2.5\times 10^5,|E|=|V|-1,\sum |S|\le 5\times 10^5$。

显然的虚树题。每次询问，对$S\cup\{1\}$建虚树，边权置为两点间边权最小值。那么我们就只需要在这个虚树做原问题即可。由于虚树的规模是$O(|S|)$，考虑到排序的复杂度，则总复杂度为$O(\sum |S|\log_2|V|)$。

代码

「例 2」 ZR982 黄队

有一棵$n$个节点的树，其中所有的树边$1$到$n−1$标号。定义$\delta(v,r)$为$v$经过由标号不超过$r$的边构成的路径到达的点集。

现在有$q$个询问，每个询问给你一组点$v_1,v_2,\cdots,v_k$，求$(r_1,r_2,\cdots ,r_k)$这样的$k$元组个数，满足$0\le r_i\le n−1$且$δ(v_i,r_i)$这些点集两两不交。

由于答案很大，请输出对$10^9+7$取模的值。

$1\leq n, q, \sum k\leq 2\times 10^5$.

首先思考$\delta(u,x)$和$\delta(v,y)$不相交的条件是什么。设$w(u,v)$表示$u$到$v$的边的编号最大值，那么充要条件就是$x<w(u,v)$且$y<w(u,v)$。

题目中要求的是两两不交，那么意味着$r_i<\min_{1\le j\le k,j\ne i} w(v_i,v_j)$。

考虑离线并查集。把边权从小到大排序。那么考虑当前$(u,v,w)$这条边，则$u$的连通块和$v$的连通块边权都小于$w$，因此如果$u$中只有一个关键点，$v$中有至少一个关键点，那么$u$的关键点对应的$r$的限制就是$w$。对称情况是一样的。其他情况，是不能确定限制的值的。

最后把限制都乘起来就是答案。

这个过程显然是可以在虚树上做的。

总复杂度$O(n+\sum k\log_2n)$。