字符串导论

本文将讲述关于字符串的基本概念以及延伸的推论。

注：如无特殊说明，通常情况下$[l,r]$表示整数区间（即$\{l,l+1,\cdots,r\}$）而不是实数区间。类似地，$[l,r)=\{l,l+1,\cdots,r-1\}$。

基本定义与符号表示

字符串：字符串通常使用单个字母表示，如$S$，$s$，$t$。

长度：字符串$S$的长度（Length）表示为$|S|$。

字符：字符串$S$从左到右第$i$个字符记为$S[i]$。如果没有特殊说明，通常是 1 作为起始下标。

子串：$S$中第$l$个字符到第$r$个字符构成的串称作$S$的子串（Substring），记作$S[l,r]$。其中$1\le l,r\le |S|$。

前缀：如果$l=1$，那么这个子串也被称作$S$的前缀（Prefix）。

后缀：如果$r=|S|$，那么这个子串也被称为$S$的后缀（Suffix）。

周期与 Border

Border：若对于$x(1\le x< |S|)$满足$S[1,x]=S[|S|-x+1,|S|]$，那么称$S[1,x]$是$S$的Border（也称$x$是$S$的 Border）。

周期：若对于$x(1\le x\le |S|)$，使得$\forall i\in[1,|S|-x],S[i]=S[i+x]$，那么称$S[1,x]$是$S$的周期（Period），也称$x$是$S$的周期。

记$S$的最小周期为$\text{per}(S)$。

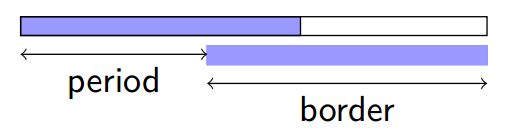
每个周期（除了$x=|S|$的周期）都对应了一个 Border。具体地，周期$x$对应了 Border$|S|-x$。

求所有 Border：KMP 算法不停跳 Fail 指针即可。

周期引理

弱周期引理（Weak Periodicity Lemma）：若$p,q$都是$S$的周期且$p+q\le |S|$，则$\gcd(p,q)$也是$S$的周期。

证明：不妨设$p<q$。设$d=q-p$。$\forall i\in[1,|S|-d]$，发现$i+q\le |S|$和$i-p\ge 1$一定满足其中一个。因此可以退出$S[i]=S[i+d]$。即$d$是$S$的周期。那么辗转相减即可证明。

周期引理（Periodicity Lemma）：若$p,q$都是$S$的周期且$p+q-\gcd(p,q)\le |S|$，则$\gcd(p,q)$也是$S$的周期。

字符串匹配

引理 1（等差数列引理）：字符串$S,T$满足$2|S|\ge |T|$，则$S$在$T$中的所有匹配位置构成一个等差数列。

证明：

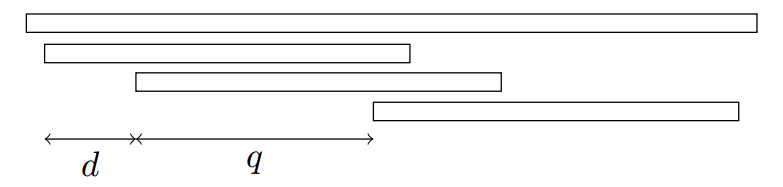
考虑其中的 3 次匹配：第 1 次，第 2 次和最后一次。设它们的间距分别是$d,q$。

根据周期的定义得，$d,q$都是$S$的周期。

由于$2|S|\ge |T|$，因此$d+q\le |S|$。因此根据周期引理，$\gcd(d,q)$也是$|S|$的周期。

因此不难证明，（设第一次匹配的位置是$x_0$）$x_0,x_0+\gcd(d,q),\cdots,x_0+d+q$都是匹配位置。即构成一个公差为$\gcd(d,q)$的等差数列。更严格地说，是构成一个公差为$d$的等差数列。

引理 2（公差引理）：字符串$S,T$满足$2|S|\ge |T|$，则$S$在$T$中的所有匹配位置构成一个等差数列。若等差数列至少有 3 项，则其公差$d$等于$S$的最小周期$\text{per}(S)$。此时易知$2d\le |S|$。

仅含两项时不一定成立，如$S=\text{aabaa},T=\text{aabaaabaa}$。

Border 的结构

引理（等差数列引理）：字符串$S$的所有长度不小于$\frac{|S|}{2}$的 Border 的长度构成等差数列。

证明：

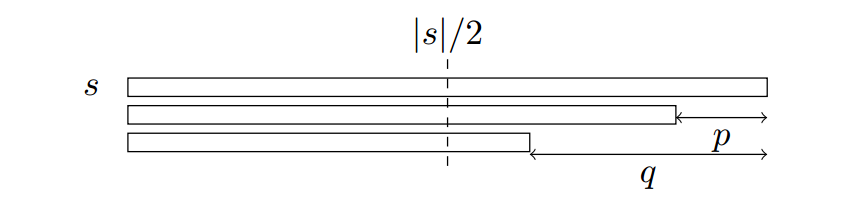
我们知道每个周期都对应一个 Border。而长度不小于$\frac{|S|}{2}$的 Border 对应的周期满足周期引理。因此周期是等差数列，则得证。

上述引理刻画了长度不小于$\frac{|S|}{2}$的 Border 的结构。那么对于长度更小的 Border 呢？

我们将$S$的所有 Border 按长度$x$分类，有两种情况：

1. $x\in[2^{i-1},2^i)$，其中$2^i-1<|S|$；
2. $x\in[2^k,|S|)$，其中$2^k\ge \frac{|S|}{2}$。

对于第二种情况，我们使用上述引理即可。那么考虑第一种情况：

容易证明，如果存在 Border 的长度在$[2^{i-1},2^i)$，那么对于$S[1,2^i]$使用上述引理即可证明，$[2^{i-1},2^i)$中的 Border 也构成等差数列。

推论：字符串$S$的所有 Border 按长度排序后可以分成$O(\log_2|S|)$段，使得每一段都是等差数列。

子串 Border 查询

给出长度为$n$的字符串$S$，$q$次询问形如$(l,r)$，求$S[l,r]$的子串的所有 Border（等价于周期），用$O(\log_2n)$个等差数列的形式表示。

对于询问$S[l,r]$，设$t=S[l,r],m=|t|$。仍然按照 Border 长度分成两类：

1. $x\in[2^{i-1},2^i)$，其中$2^i-1<m$。
2. $x\in[2^i,m)$，其中$2^{i}\ge \frac{m}{2}$。

Case 1

$x\in[2^{i-1},2^i)$，其中$2^i-1<m$。

如图的$x$是一个满足要求的 Border。那么容易发现$t[1,2^{i-1}]$是$x$的前缀，而$t[m-2^{i-1}+1,m]$是$x$的后缀。

因此，不妨求出$t[1,2^{i-1}]$在$t[m-2^i+1,m]$中匹配的位置的集合$A$，以及$t[m-2^{i-1}+1,m]$在$t[1,2^i]$中匹配的位置的集合$B$。把$A$做一下翻转和移位之后与$B$取交集就是我们要求的了（事实上也是等差数列的交）。

因此我们的问题转化为：

询问子串$S[a,a+2^{j-1}-1]$在$S[b,b+2^j-1]$中匹配的位置集合（等差数列形式）。

显然我们只需要求出它匹配的第一次，第二次和最后一次即可。换言之问题转化为

询问子串$S[a,a+2^{j-1}-1]$在位置$x$后匹配的第一个位置 / 在$x$前匹配的最后一个位置。

用$R(a,j)$表示子串$S[a,a+2^{j}-1]$，即长度为 2 的幂的子串。这类子串的个数是$O(n\log_2n)$的。因此我们求出它们的字典序排名，把排名相同的放一起按照出现位置排序。然后询问的时候在这个序列上二分即可。排序的过程和后缀数组构建的过程类似。

而且由于长度不同的子串排名一定不同，因此我们可以构建$O(\log_2n)$个序列（相当于是把后缀数组的构建过程记录下来）来处理询问。

那么求出了$A$和$B$，如何求$A$和$B$的交集？也就是求两个等差数列的交集。

如果公差相等那么容易$O(1)$求交集。

引理：四个字符串$x_1,x_2,y_1,y_2$满足$|x_1|=|y_1|\ge |x_2|=|y_2|$，且$x_1$在$y_2y_1$中匹配至少 3 次，$y_1$在$x_1x_2$中匹配至少 3 次，则$\text{per}(x_1)=\text{per}(y_1)$，即最小周期相等。

反证：不妨设$\text{per}(x_1)>\text{per}(y_1)$。

设$x_1$的最后一次匹配与$y_1$的交是$z$。则$\text{per}(z)=\text{per}(x_1)$。

由字符串匹配的公差引理，$|z|\ge 2\text{per}(z)>\text{per}(x_1)+\text{per}(y_1)$。

因此$\gcd(\text{per}(x_1),\text{per}(y_1))$也是$z$的周期。但$\gcd(\text{per}(x_1),\text{per}(y_1))<\text{per}(z)$，矛盾。

因此我们证明了$A$和$B$如果是两个等差数列且长度超过 3，那么公差一定相等。因此求交集的复杂度是$O(1)$的。

综上，我们可以在$O(\log_2n)$的时间内处理$x\in[2^{i-1},2^i)$的情况。

Case 2

$x\in[2^i,n)$，其中$2^{i}\ge \frac{m}{2}$。

即求长度不小于$2^i$的 Border 集合。与 Case 1 做法相同。

综上，该算法空间复杂度$O(n\log_2n)$，时间复杂度$O(n\log_2n+q\log_2^2n)$。

习题：2015-2016 Petrozavodsk Winter Training Camp, Moscow SU Trinity Contest : D Deep Purple 代码

参考文献

字符串算法选讲，金策，清华大学交叉信息研究院，February 3, 2017