2021 五月训练日志

PKUSC2018 PKUSC

PKUSC 计算几何 圆

暴力。把多边形拆成有向边，问题转化为计算一个线段与圆的交（交集是线段）。这个可以做一个类似区别交的东西（这里的区间长度定义为是端点的辐角差）。

时间复杂度$O(nm)$。

细节不多。见代码。

代码

NOI2019 回家路线

NOI 斜率优化 李超树 DAG

首先，小猫走的路径是没有环的（时间不能倒流）。因此实质上本题的图是一个 DAG。

更具体地说，我们用二元组$(u, t)$表示「在时刻$t$到达结点$u$」。将题面中的模型转化为点集为$(u, t)$的图，就是一个 DAG。问题转化为求 DAG 上从$(0, 0)$到$(n, ?)$的最小代价。

本题的代价是与等待时间的连续段有关的，难以均摊到每条边上。换句话说，你没法最短路，除非你暴力建$O(n^2)$条边。不过注意到每次等待只会发生在单个结点上。因此我们将视角切换到一个结点$u$上。则在这个结点上按照时间顺序会有两种事件：列车到站和列车出发。

因此我们考虑在时刻$t_i$到达$u$，花费的最小代价设为$c_i$，而时刻$t_j$有另一列车从$u$出发（$t_i\le t_j$）于$t_k$时刻到达$v$。则到达$(v, t_k)$的代价更新为

$$A(t_j - t_i)^2 + B(t_j - t_i) + C$$

这是一个典型的斜率优化转移。

在实现的时候我们需要开$n$个队列（数组）。

时间复杂度$O(m\log_2m)$，如果使用线性的排序方式可以做到$O(m)$。

代码

注：斜率优化维护下凸壳时，在插入点的时候，对于横坐标相等的情况要特判：

#define check(X, Y, Z) (Y.x == Z.x ? (Y.y < Z.y) : (det(Vec(X, Y), Vec(Y, Z)) > 0))

NOI2019 序列

NOI 模拟费用流 贪心

首先容易想到一个费用流做法，建模类似这样

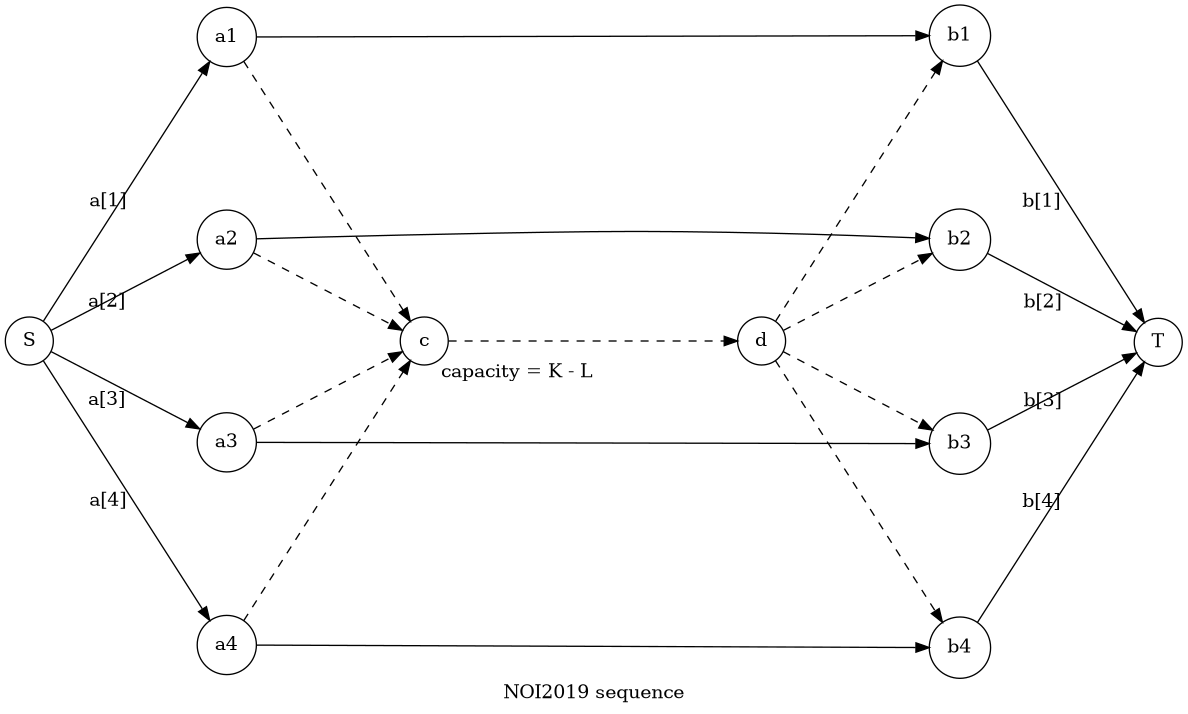
虚线部分表示选择不一定匹配的两个。

写得好应该可以获得$64$分。

满分做法是考虑优化计算费用流的过程。也就是说我们不使用常规的费用流算法，而是根据本题中费用流模型的特殊结构，设计算法模拟费用流的过程。

就本题而言我们模拟増广路算法。増广路算法的特征是每次找费用的最短路，也就是贪心。

观察发现，每次増广相当于是左边选了一个$a_x$右边选了一个$b_y$。中间怎么流我们其实不关心，因为没有费用，只有一个限制：满足$(c,d)$这条边的容量限制。因此我们的问题可以抽象为一个贪心选数的问题。

如果$(c, d)$这条边没有满流，那么増广过程等价于贪心选择$a$的最大值和$b$的最大值，直到满流。

如果满流，那么我们有三种増广路（选数）类型：

1. 选择两个相匹配的数$(a_i, b_i)$，且这两个数之前没有被选过。
2. 对于$(a_i, b_i)$其中$a_i$被选，$b_i$未选。那么我们选上$b_i$，含义是给一个$S\to a_i\to b_i\to T$的流，踢掉原本$a_i \to c$的流。这时$c$的入流少了$1$，那么我们再从未选的$a_i$中贪心拿最大的即可。
3. 对于$(a_i, b_i)$其中$a_i$未选，$b_i$被选的情况同理。

$3$种情况取最优即可。

容易发现上述増广过程可以数据结构简单维护。

时间复杂度$O(Tn\log_2n)$。

代码

NOI2019 弹跳

NOI K-D Tree 最短路

看起来是个单源最短路。由于边权非负，容易想到 Dijkstra 算法。

但是直接建图边数太多，如果使用二维线段树或者树套树优化建图会使得复杂度达到$O(m\log^2n)$的量级，而且还容易被卡空间。

因此我们考虑优化算法过程。基本的 Dijkstra 算法中我们维护一个小根堆，堆中存放形如$(u, d)$的二元组，表示到达$u$的最短距离是$d$。

由于本题中连出的边是一个矩形的范围，因此容易想到将二元组魔改成$(R, d)$，表示到达矩阵$R$中还未被访问（入堆）的点的最短距离是$d$。因为 Dijkstra 算法中每个点只会被访问一次，因此$R$中已经被访问过的点的最短路距离一定小于等于$d$，所以我们可以不考虑这些点。

因此问题转化为：如何寻找一个矩阵中未被访问过的点。这个可以树套树或者 K-D Tree。K-D Tree 空间更小。每次我们找到一个点后将其入堆，然后把它标记为已访问过。如果 K-D Tree 上某个结点代表的矩阵内的所有结点都被访问过了，就没必要遍历这个子树了。

K-D Tree 定位单个点的复杂度是$O(\log n)$的，而每个点最多被定位一次。因此总复杂度$O(n\log n + m\log n)$。

代码

NOI2019 斗主地

插值 数学 猜结论

一句话：一次函数洗牌之后的期望还是一次函数，二次函数洗牌之后的期望还是二次函数。

这个结论并没有那么好猜。证明的话可以从一次函数的角度，写一个归纳法，发现可以拆成若干个范德蒙德恒等式的和。二次函数可以差分成一个一次函数来理解。

其实有另外一种更意识流的理解：洗牌本质上是把这个函数分成前后两段，然后均匀地混合在一起。所以一次函数混合后仍是一次函数，二次函数混合后仍是二次函数。

详细证明没啥营养。

代码

PKUSC2018 星际穿越

倍增

首先可以发现，固定$u$。从$u$走到$i$（$i < u$） 的最短步数随$i$增大是逐渐减小（不上升）的。

因此我们可以设$f(u, i)$表示从$u$出发走$i$步走到的最靠左的点。

容易发现$f(u, 1) = l_u$。

可以发现$f(u, 2) = \min_{u \le v} l_v$。进而$f(u, 3) = \min_{f(u, 2) \le v} l_v$。

也就是说除了第一步比较特殊，之后的转移是类似的。因此我们对之后的部分做一个倍增即可。

设$f'(u, j)$表示从满足$u\le v$的$v$出发走$2^j$步到达的最左端的点。设$g(u, j)$表示从满足$u\le v$的$v$出发，走到$u - 1, u - 2, \ldots, f'(u, 2^j)$的最短步数的和。

转移是 trivial 的。

注意特殊处理第一步。也就是说在回答询问的时候我们是从$l_u$出发。然后再加上$u$到$l_u$的贡献。

代码