线性代数入门

遇到一道毒瘤的数理知识题，就有了本文。

矩阵

将一些元素排列成若干行，每行放上相同数量的元素，就是一个矩阵（Matrix）。

矩阵通常用大写字母表示。一个矩阵 $A$ 从左上角数的第 $i$ 行第 $j$ 列的数称作第 $i,j$ 项，记作 $A_{i,j}$ 或 $A_{ij}$ 。

如果 $A$ 的元素可以用只与行数和列数有关的函数 $f$ 表示，则可以用 $A=[f(i,j)]_{m\times n}$ 表示。其中 $m$ 表示行数， $n$ 表示列数。

对于 $m=n$ 的矩阵我们称之为方阵（方块矩阵）。

矩阵基本操作

加法、标量乘法、转置

加法：对于矩阵 $A_{m\times n},B_{m\times n}$ ，定义矩阵加法为 $A$ 和 $B$ 对应位置上的元素相加。即 $A+B=[A_{i,j}+B_{i,j}]_{m\times n}$ 。

标量乘法（Scalar multiplication）：对于矩阵 $A_{m\times n}$ 和标量 $c$ ，他们相乘的结果是 $Ac=[A_{i,j}\cdot c]_{m\times n}$ 。

转置（Transposition）：对于矩阵 $A_{m\times n}$ ，其转置矩阵记作 $A^T$ ，且 $A^T=[A_{j,i}]_{n\times m}$ 。即横竖翻转。

矩阵乘法

定义 $A_{n\times m}$ 和 $B_{m\times k}$ 的矩阵乘法为

$AB=\left[ \sum_{x=1}^mA_{i,x}B_{x,j} \right]_{n\times k}$

其中 $i\in[1,n],j\in[1,k]$ 。

分配律： $(A+B)C=AC+BC$ 。
结合律： $A(BC)=(AB)C$ 。
矩阵乘法不具备交换律。

矩阵初等变换

矩阵初等变换有三种，分行操作和列操作。不过行和列是对称的。

行交换：将矩阵 $A_{n\times m}$ 的第 $i$ 行和第 $j(i\ne j)$ 行交换。记作 $R_i\leftrightarrow R_j$ 。
行数乘：将第 $i$ 行的每个元素都乘上一个非 $0$ 常数 $k$ ，记作 $kR_i\to R_i,k\ne 0$ 。
行加法：第 $j$ 行的 $k(k\ne 0)$ 倍加到第 $i$ 行上，记作 $R_i+kR_j\to R_i,i\ne j$ 。

方阵初等变换

对于方阵而言，由于两个方阵的矩阵乘法不改变方阵的形状，因此我们可以用矩阵乘法表示方阵的初等变换。

对于 $R_i\leftrightarrow R_j$ ，等价于 $A_{n\times n}$ 左乘一个 $B_{n\times n}$ 的矩阵，满足

$B_{x,y}=\begin{cases} 1 & x=i,y=j\\ 1 & x=j,y=i\\ 1 & x=y,x\ne i,x\ne j\\ 0 & \text{Otherwise} \end{cases}$

对于 $kR_i\to R_i,k\ne 0$ 操作， $B$ 的条件为

$B_{x,y}=\begin{cases} k & x=y,x=i\\ 1 & x=y,x\ne i\\ 0 & \text{Otherwise} \end{cases}$

对于 $R_i+kR_j\to R_i,i\ne j$ ， $B$ 的条件为

$B_{x,y}=\begin{cases} k & x=i,y=j\\ 1 & x=y\\ 0 & \text{Otherwise} \end{cases}$

对于初等列变换，则可以表示为 $A$ 右乘一个矩阵 $B$ 。设 $C_i$ 表示矩阵的第 $i$ 列。

对于 $C_i\leftrightarrow C_j$ ， $B$ 的条件与 $R_i\leftrightarrow R_j$ 相同：

$B_{x,y}=\begin{cases} 1 & x=i,y=j\\ 1 & x=j,y=i\\ 1 & x=y,x\ne i,x\ne j\\ 0 & \text{Otherwise} \end{cases}$

对于 $kC_i\to C_i,k\ne 0$ ， $B$ 的条件与 $kR_i\to R_i,k\ne 0$ 相同：

$B_{x,y}=\begin{cases} k & x=i,y=j\\ 1 & x=y\\ 0 & \text{Otherwise} \end{cases}$

对于 $C_i+kC_j\to C_i,i\ne j$ ， $B$ 的条件是 $R_i+kR_j\to R_i,i\ne j$ 的转置：

$B_{x,y}=\begin{cases} k & x=j,y=i\\ 1 & x=y\\ 0 & \text{Otherwise} \end{cases}$

矩阵求逆

定义单位矩阵（Identity Matrix）为主对角线上元素为 $1$ ，其他元素为 $0$ 的方阵，记作 $I$ 。

定义 $A$ 矩阵的逆矩阵 $B$ 为使得 $AB=I$ 的矩阵。若存在这样的 $B$ 矩阵，称 $A$ 可逆。 $A$ 的逆矩阵记作 $A^{-1}=B$ 。

定义符号 $(A | B)$ 表示在 $A_{n\times n}$ 矩阵右边放置 $B_{n\times n}$ 矩阵，形成 $n\times 2n$ 的矩阵。

那么我们使用高斯消元将 $(A|I)$ 中的 $A$ 消成 $I$ ，得到 $(I|B)$ ，那么这里的 $B$ 就是 $A^{-1}$ 。若 $A$ 消不成 $I$ 则 $A$ 不可逆。

相似矩阵

相似矩阵（similar matrix）是指存在相似关系的矩阵。两个 $n\times n$ 的方阵 $A$ 和 $B$ 为相似矩阵当且仅当存在 $n\times n$ 的可逆矩阵 $P$ 满足

$P^{-1}AP=B$

相似矩阵的秩、行列式、特征值、特征多项式相同。

行列式

行列式通常是对于方阵定义的。

方阵 $A_{n\times n}$ 的行列式（Determinant）是一个将其映射到标量的函数，记作 $\det(A)$ 或者 $|A|$ 。通常可以将其理解为是高维空间的欧氏体积。

定义 $P_n$ 表示所有 $n!$ 个长度为 $n$ 的排列 $p$ 构成的集合。矩阵的行列式定义为：

$|A|=\sum_{p\in P_n}\operatorname{sgn}(p)\prod_{i=1}^nA_{i,p_i}$

其中 $\operatorname{sgn}$ 表示排列的逆序对个数对 $-1$ 的幂。即设 $N(p)$ 表示排列 $p$ 的逆序对个数，则 $\operatorname{sgn}(p)=(-1)^{N(p)}$ 。

行列式操作

方阵乘积的行列式等于行列式的乘积： $|AB|=|A||B|$ 。证明

若 $A$ 可逆，则 $|A^{-1}|=|A|^{-1}$ 。

行列式的计算

直接计算

根据行列式的公式，易得

对方阵做行（列）交换，行列式反号；
对方阵做行（列）数乘，行列式乘上同样的常数。
对方阵做行（列）加法，行列式不变；
对于上（下）三角矩阵，其行列式为主对角线上元素的积。

因此可以简单地使用高斯消元在 $O(n^3)$ 的时间内求出行列式。

拆行列式

行列式按行拆开：设 $a_{ki}=b_i+c_i$ ，那么有

$|A|= \left|\begin{matrix} a_{11} & a_{12} & \cdots & a_{1n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{k1} & a_{k2} & \cdots & a_{kn}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{matrix}\right| = \left|\begin{matrix} a_{11} & a_{12} & \cdots & a_{1n}\\ \vdots & \vdots & \ddots & \vdots\\ b_{1} & b_{2} & \cdots & b_{n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{matrix}\right| + \left|\begin{matrix} a_{11} & a_{12} & \cdots & a_{1n}\\ \vdots & \vdots & \ddots & \vdots\\ c_{1} & c_{2} & \cdots & c_{n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{matrix}\right|$

按列拆开同理。

余子式与伴随矩阵

余子式：对于矩阵 $A$ ， $A_{ij}$ 的余子式 $M_{ij}$ 定义为 $A$ 去掉第 $i$ 行第 $j$ 列的矩阵的行列式。

代数余子式：对于矩阵 $A$ ， $A_{ij}$ 的代数余子式 $C_{ij}=(-1)^{i+j}M_{ij}$ 。

代数余子式求行列式： $\forall k,|A|=\sum_{i=1}^nA_{ki}C_{ki}$ 。

余子矩阵：代数余子式构成的矩阵 $C=[C_{ij}]$ 。

伴随矩阵： $A$ 的伴随矩阵定义为 $A$ 的余子矩阵的转置，即 $C^T$ ，记为 $\operatorname{adj}(A)$ 。

伴随矩阵关于逆矩阵的性质：如果 $A$ 可逆，那么 $\operatorname{adj}(A^{-1})=\operatorname{adj}(A)^{-1}=\dfrac{A}{|A|}$ 。

其他环上行列式的计算

对于环 $(\oplus, \otimes)$ 上的 $n$ 阶方矩阵 $M$ ，其行列式记作

$|M|=\bigoplus_{p\in P_n}\operatorname{sgn}(p)\bigotimes_{i=1}^nA_{i,p_i}$

那么对于这种矩阵的高斯消元，要点是：消成 $\oplus$ 对应的单位元。

可以类比加法乘法环的高斯消元，把除法换成求逆之类的。

矩阵特征值与特征多项式

特征值与特征向量

对于矩阵 $A_{n\times n}$ ，若存在向量 $\mathbf{v}_{n}$ 和标量 $\lambda$ 满足

$\begin{bmatrix} A_{11} & A_{12} & \cdots & A_{1n}\\ A_{21} & A_{22} & \cdots & A_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ A_{n1} & A_{n2} & \cdots & A_{nn}\\ \end{bmatrix} \begin{bmatrix} v_{1}\\ v_{2}\\ \vdots \\ v_{n}\\ \end{bmatrix} = \begin{bmatrix} \lambda v_{1}\\ \lambda v_{2}\\ \vdots \\ \lambda v_{n}\\ \end{bmatrix}$

即

$A\mathbf{v}=\lambda\mathbf{v}$

则称 $\mathbf{v}$ 是矩阵 $A$ 的特征向量（Eigenvector），且 $\lambda$ 是 $\mathbf{v}$ 对应的特征值（Eigenvalue, or characteristic root）。

上面的等式可以等价地写作

$(\lambda I-A)\mathbf{v}=0$

特征多项式

若 $\mathbf{v}$ 不是零向量，则 $(\lambda I-A)\mathbf{v}=0$ 的充要条件是 $|\lambda I-A|=0$ 。而 $|\lambda I-A|$ 可以表示为 $\lambda$ 的一个多项式。

根据行列式的计算公式，易知 $|\lambda I-A|$ 是一个 $n$ 次多项式。那么不妨设它的 $n$ 个零点为 $\lambda_1,\lambda_2,\cdots,\lambda_n$ ，则 $A$ 的特征多项式（Characteristic polynomial）为

$p_A(\lambda)=|\lambda I-A|=\begin{vmatrix} \lambda-A_{11} & -A_{12} & \cdots & -A_{1n}\\ -A_{21} & \lambda- A_{22} & \cdots & -A_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ -A_{n1} & -A_{n2} & \cdots & \lambda - A_{2n} \end{vmatrix}=(\lambda - \lambda _1)(\lambda - \lambda _2)\cdots (\lambda - \lambda _n)$

不妨设 $p_A(\lambda)=f_0+f_1\lambda+\cdots + f_n\lambda^n$ 。

根据特征多项式的定义，易得

$f_n=1$ ；
$f_0=(-1)^n\prod_{i=1}^n \lambda_i$ ；

特征多项式的计算

首先，你可以通过对 $(\lambda I-A)$ 高斯消元来求特征多项式，但你不能对 $A$ 高斯消元后再求 $A$ 的特征多项式，两者是不同的。

根据相似矩阵性质，我们知道与 $A$ 相似的矩阵的特征多项式是相同的。而上三角矩阵的特征多项式是很容易计算的（主对角线上的元素相乘）。因此我们可以尝试把 $A$ 化为与其相似的上三角矩阵。遗憾地是，这样的变换复杂度没有保证。不过，我们有一个类似上三角矩阵的矩阵，叫作上海森堡矩阵。而我们可以快速将 $A$ 变换为与其相似的上海森堡矩阵，然后求出上海森堡矩阵的特征多项式，也就得到了 $A$ 的特征多项式。

上海森堡矩阵

定义上海森堡矩阵（Upper Hessenberg Matrix）为方阵 $A_{n\times n}$ 满足 $\forall 1\le j<i\le n,A_{ij}=0$ 。即

$\begin{bmatrix} A_{11} & A_{12} & A_{13} & \cdots & A_{1n}\\ A_{21} & A_{22} & A_{23} & \cdots & A_{2n}\\ 0 & A_{32} & A_{33} & \cdots & A_{3n}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & A_{nn}\\ \end{bmatrix}$

也就是说主对角线下面的一条对角线也可能非 0。

如何将 $A$ 化为与其相似的上海森堡矩阵？考虑消元。

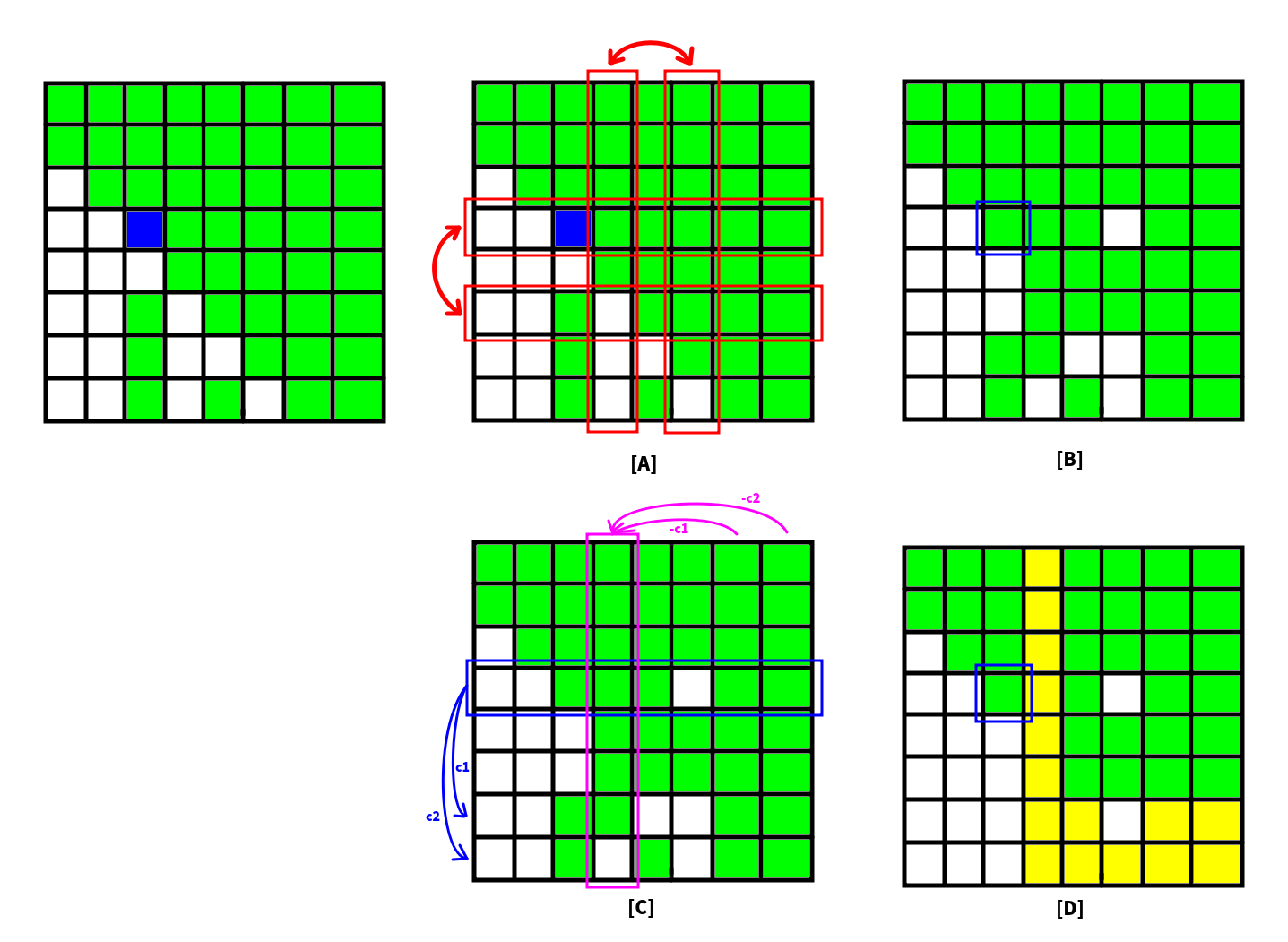
如图：

绿色表示非 $0$ 元素；
蓝色表示我们当前考虑的元素 $(i,j)(i>j)$ ；
黄色表示发生变化的元素（不确定是 $0$ 还是非 $0$ ）。

左图是我们目前的矩阵的状态。我们想将 $(i,j)$ 下方的非零元素消掉。首先若 $A_{ij}$ 是 $0$ ，我们就要找下方第 $j$ 列非 $0$ 的元素与之替换（如果找不到就不用消元了）。

图 A：假设我们找到了 $A_{kj}\ne 0(k>i)$ ，那么我们就需要做 $R_i\leftrightarrow R_k$ 的操作。而为了保证操作后的矩阵与 $A$ 相似，我们需要在右边乘上它的逆矩阵。而 $R_i\leftrightarrow R_k$ 对应的矩阵的逆矩阵是其本身。右边乘上 $R_i\leftrightarrow R_k$ 对应的矩阵，实际上就是做 $C_i\leftrightarrow C_k$ 的操作。因此在图 A 中我们进行了行交换和列交换。

图 B 是我们把 $A_{ij}$ 置为非零元素后的状态。

图 C：接下来进行消元。我们相当于做若干次行加法操作。同样的为了保证操作后的相似，我们需要右乘行加法操作的逆矩阵。而行加法操作的逆矩阵就是将 $k$ 反号后的行加法矩阵（把它减回去）。放到右边乘就对应了列加法的矩阵。因此在图 C 中我们进行了行加法和列加法操作。（同时列加法操作没有影响到第 $j$ 列。如果你想使用这个算法消成上三角矩阵，那么就会有影响）。

图 D 就是消元后的矩阵，并展示了哪些元素受到影响。

算法的伪代码描述为

$\begin{array}{r|l} \hline 1 & \textbf{Input: }\text{Matrix }A\in\mathbf{Z}_p^{n\times n}\\ 2 & \textbf{Output: }\text{Matrix }A\text{ in upper Hessenberg form with the same eigenvalues}\\ \\ 3 & \textbf{for }j=1\textbf{ to }n-2\textbf{ do}\\ 4 & \qquad \text{search for a nonzero entry }A_{i,j}\text{ where }j+1<i\le n\\ 4 & \qquad \textbf{if}\text{ found such entry }\textbf{then}\\ 5 & \qquad \qquad \textbf{do }R_i\leftrightarrow R_{j+1} \text{ and }C_i\leftrightarrow C_{j+1} \textbf{ if }A_{j+1,j}=0\\ 6 & \qquad \qquad \textbf{for }k=j+2\textbf{ to }n\textbf{ do}\\ 7 & \qquad \qquad \qquad \textbf{comment }\text{reduce using }A_{j+1,j}\text{ as pivot}\\ 8 & \qquad \qquad \qquad u\gets A_{k,j}A_{j+1,j}^{-1}\\ 9 & \qquad \qquad \qquad R_k \gets R_k-uR_{j+1}\\ 10 & \qquad \qquad \qquad C_{j+1} \gets C_{j+1}+uC_{k}\\ 11 & \qquad \qquad \textbf{end for} \\ 12 & \qquad \textbf{end if}\\ 13 & \qquad \textbf{comment }\text{now the first }j\text{ columns of }A\text{ is in upper Hessenberg form}\\ 14 & \textbf{end for} \\ \hline \end{array}$

时间复杂度 $O(n^3)$ 。

上海森堡矩阵的行列式

显然，若 $A$ 是上海森堡矩阵，则 $(\lambda I-A)$ 也是上海森堡矩阵。因此我们只需要能快速求出上海森堡矩阵的行列式即可。

不妨考虑我将 $A$ 的行列式按第一列展开。因为第一列只有两个非 $0$ 元素：

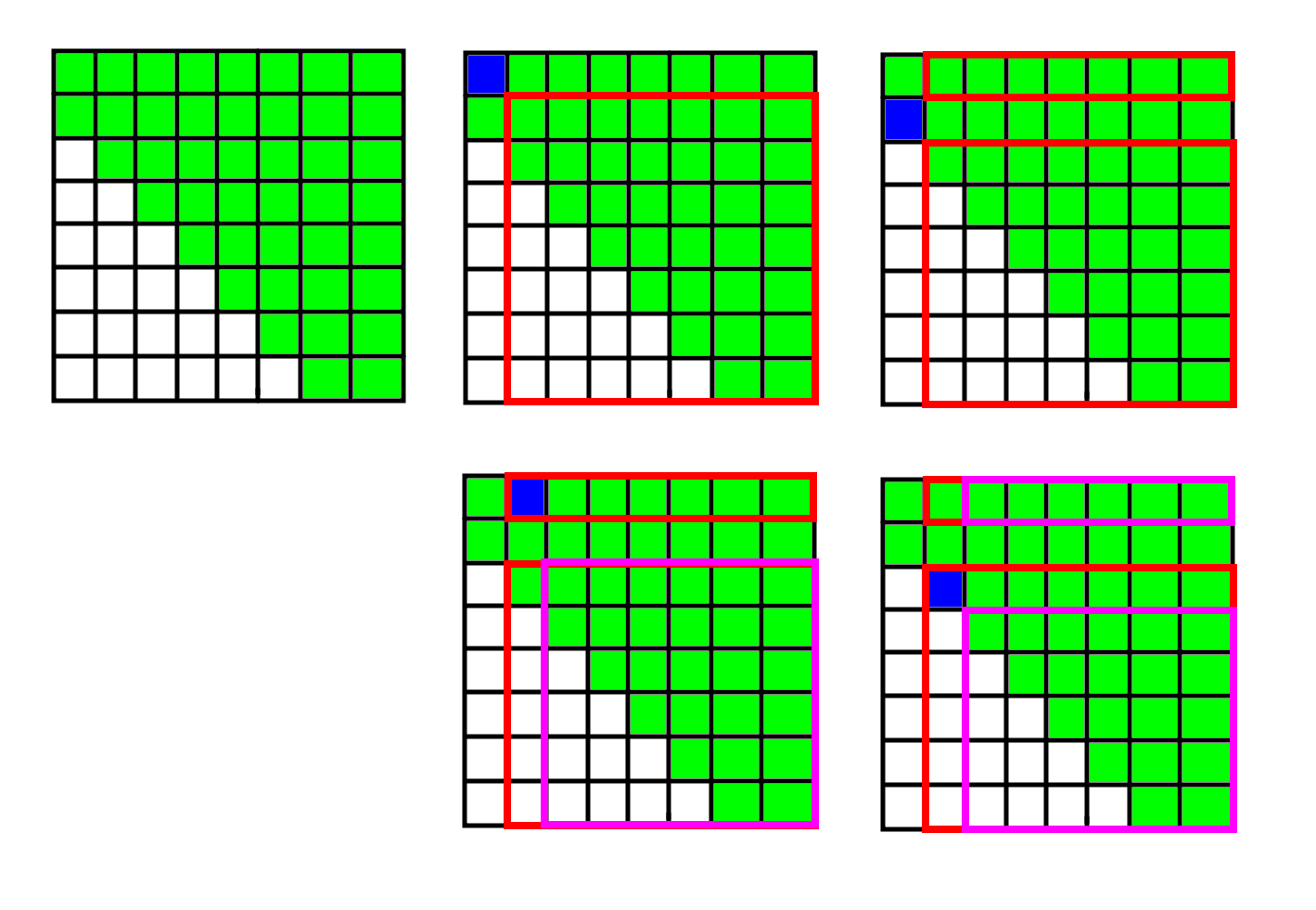
设 $p_i$ 表示第 $i$ 到第 $n$ 行，第 $i$ 列到第 $n$ 列的子矩阵的行列式。考虑求 $p_1$ 。那么我们按第 $1$ 列展开，就得到 $p_1=A_{11}p_2-A_{21}|\text{red}|$ 。而 $\text{red}$ 子矩阵的行列式也可以按列展开！于是 $|\text{red}|=A_{12}p_3-A_{32}|\text{pink}|$ 。那么可以继续这样展开下去。这样就可以求出 $p_1$ 也就是原矩阵的行列式了。实现的时候倒着做一次循环就行了。

复杂度也是 $O(n^3)$ 的，因为多项式长度是 $O(n)$ 的。

代码

哈密尔顿 - 凯莱定理

哈密尔顿–凯莱定理（Cayley–Hamilton theorem）：对于矩阵 $A$ 的特征多项式 $f(\lambda)$ ，有 $f(A)=O$ 。这里的 $f(A)$ 表示说把多项式放在矩阵环的意义下进行， $O$ 表示全 $0$ 矩阵，常数项 $a_0$ 可以理解为 $a_0I$ ， $I$ 是单位矩阵。

常系数齐次线性递推

给出 $x_0,\cdots,x_{k-1}$ 和 $c_1,c_2,\cdots,c_k$ ，且定义递推式
$x_n=c_1x_{n-1}+\cdots + c_kx_{n-k}$
求 $x_n$ 。

思路一

首先我们可以用矩阵乘法的形式描述这个过程：

$\begin{bmatrix} x_n\\ x_{n-1}\\ \vdots\\ x_{n-k+2}\\ x_{n-k+1} \end{bmatrix} =A\begin{bmatrix} x_{n-1}\\ x_{n-2}\\ \vdots\\ x_{n-k+1}\\ x_{n-k} \end{bmatrix}= \begin{bmatrix} c_1 & c_2 &\cdots & c_{k-1} &c_k\\ 1 & 0 &\cdots & 0 & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 &\cdots & 0 & 0\\ 0 & 0 &\cdots & 1 & 0\\ \end{bmatrix} \begin{bmatrix} x_{n-1}\\ x_{n-2}\\ \vdots\\ x_{n-k+1}\\ x_{n-k} \end{bmatrix}$

设 $V_n=[x_{n+k-1},x_{n+k-2},\cdots,x_{n+1},x_{n}]^T$ 。上式可以等价地表示为 $V_n=AV_{n-1}$ 。

那么初始向量为 $V_0=[x_{k-1},x_{k-2},\cdots,x_0]^T$ 。显然我们求出 $V_n=A^nV_0$ ，这样也就求出 $x_n$ 了。

直接做矩阵乘法，用矩阵快速幂的复杂度是 $O(k^3\log_2n)$ 的。

考虑到这里的 A 是一个 Frobenius matrix。可以得到它的特征多项式

$\begin{aligned} f(x)&=|xI-A|\\ &=x^k-c_1x^{k-1}-c_2x^{k-2}-\cdots - c_{k-1}x-c_k \end{aligned}$

根据 Hamilton Cayley Theorem，有 $f(A)=0$ 。考虑计算 $A^n$ 。

从多项式的角度理解，我们可以把 $A^n$ 表示为 $f(A)Q(A)+R(A)$ 的形式，其中 $\deg R<\deg f$ 。即 $R(x)=x^n\bmod f(x)$ 。而由于 $f(A)=0$ ，因此可以得到 $A^n=R(A)$ 。我们可以直接快速幂，把取模的部分改成多项式取模而在 $O(k^2\log_2n)$ 或者 $O(k\log_2k\log_2n)$ 的时间内求出 $R(x)$ 。求出来之后，设

$R(x)=\sum_{i=0}^{k-1}r_ix^i$

则

$V_n=A^{n}V_0=\sum_{i=0}^{k-1}r_iA^iV_0=\sum_{i=0}^{k-1}r_iV_i$

由于我们并不需要求出整个向量，我们只需要求出 $V_i$ 的最后一项。而 $V_0,\cdots,V_{k-1}$ 的最后一项恰好对应 $x_1,\cdots,x_k$ ，因此直接代入上式即可。

这样的复杂度是 $O(k^2\log_2n)$ 或者 $O(k\log_2k\log_2n)$ 的。

Luogu4723 代码

思路二

实际上我们有更简单的理解方式。

因为 $x_n=c_1x_{n-1}+\cdots + c_kx_{n-k}$ ，那么我们继续把 $x_{n-1}$ 写成 $\sum c_ix_{n-1-i}$ 的形式，然后把 $x_{n-2}$ 写成 $\sum c_ix_{n-2-i}$ 的形式，这样一直下去，就可以把 $x_n$ 写成关于 $x_0,\cdots,x_{k-1}$ 的答案。

把这个过程写成一个代码，就是多项式取模的形式。