类欧几里德算法小结

以前学的一直是推式子版的类欧，难记又难写。现在学会了几何意义版本，就写个总结。

问题引入

对于正整数参数$a, b, c$和非负整数$n$，我们想要计算$f(a, b, c, n) = \sum_{i=0}^n \lfloor \frac{ai+b}{c} \rfloor$。

考虑其几何意义，设$l: y=\frac{ax+b}{c}$。我们要求的实际上是二维平面上$l$，$x$轴，$y$轴和$x=n$这$4$条直线围成的梯形中整点的数量。细节地说，对于边界上的点，$x$轴上的点不能取，其他三条线上的点都能取。

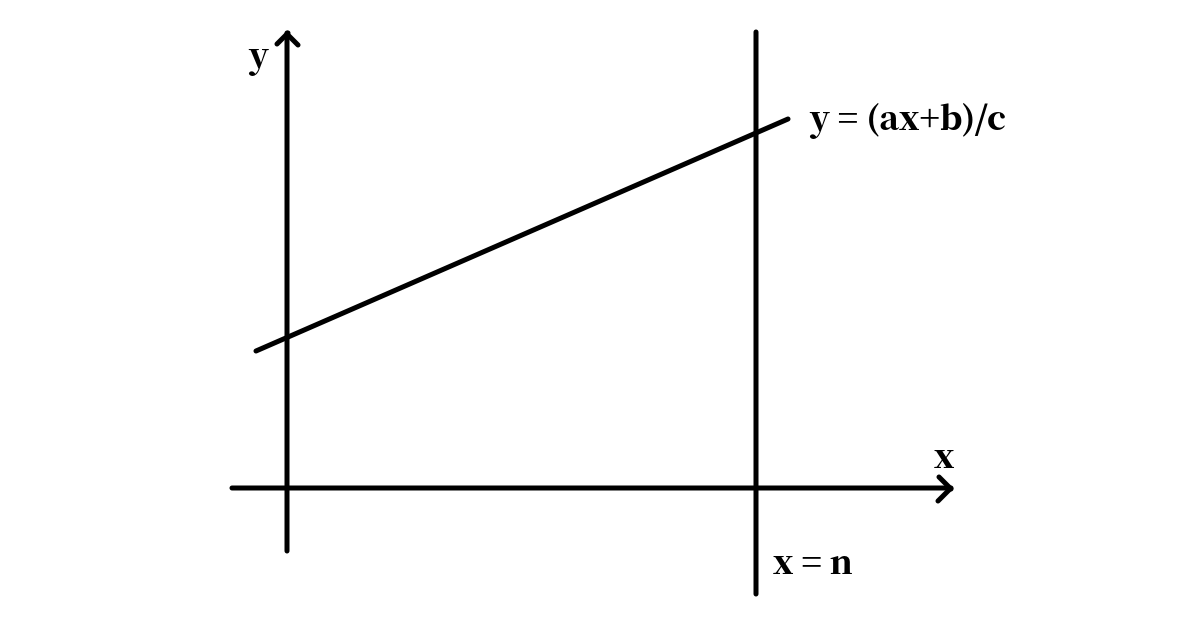
接下来我们做一些分类讨论，目的是减小问题规模，划分出子问题。

当$b\ge c$时，我们可以截一个矩形出来：

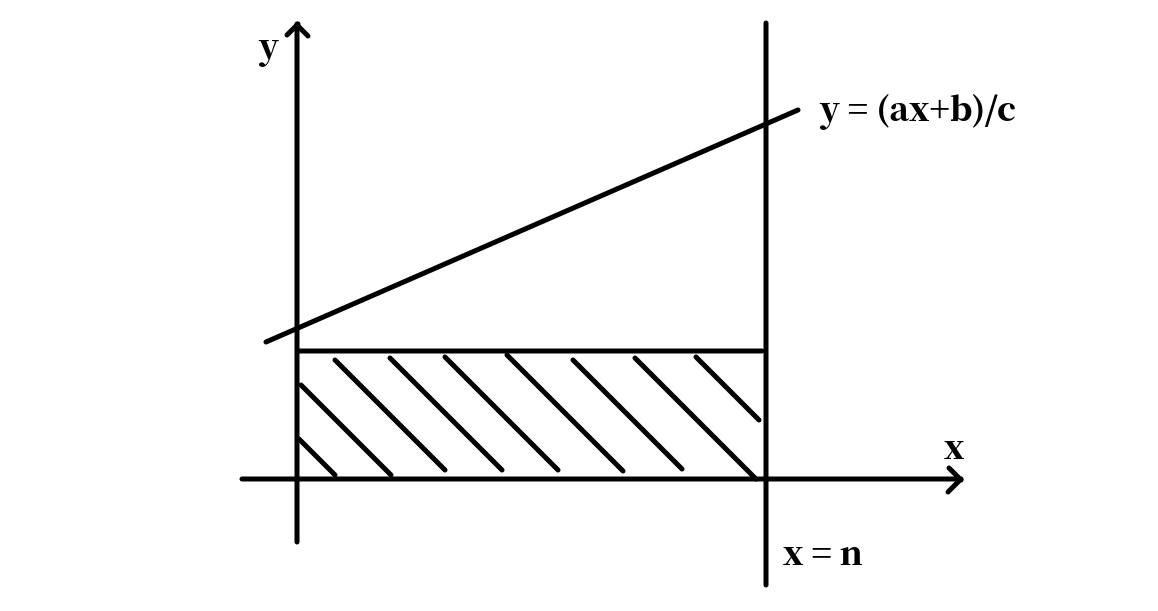
然后问题转化为求上面那个梯形里的整点数。因此有

$$f(a, b, c, n) = \left\lfloor\frac{b}{c}\right\rfloor (n+1) + f(a, b\bmod c, c, n)$$

当$a\ge c$时，我们引一条过原点斜率为整数的直线$l_2: y = kx$，其中$k = \left\lfloor\frac{a}{c}\right\rfloor$。那么我们先考虑求$l_2$下方的整点数，然后求$l$与$l_2$之间的整点数。

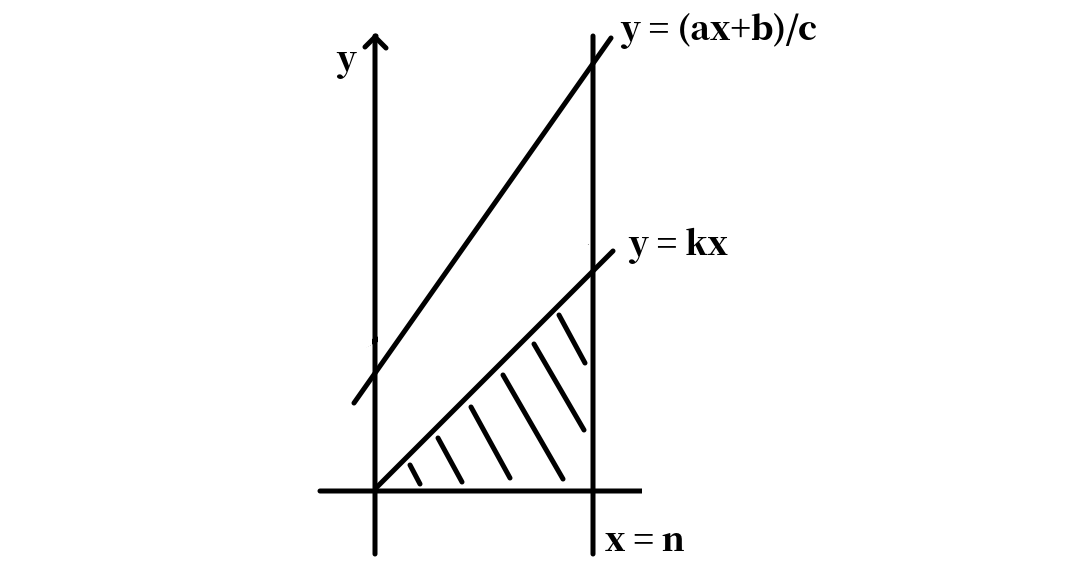
前者可以用等差数列公式求得$\frac{1}{2}\left\lfloor\frac{a}{c}\right\rfloor n(n+1)$。对于后者，考虑将整个平面上的点做一个映射：$(x, y) \to (x, y-kx)$。容易发现这个映射的实质是把上面的那个梯形变成紧靠$x$轴的直角梯形。而$l$经过映射后得到的直线变成了$y=\frac{ax+b}{c} - kx = \frac{(a\bmod c)x+b}{c}$。因此

$$f(a, b, c, n) = f(a\bmod c, b, c, n) + \frac{1}{2}\left\lfloor\frac{a}{c}\right\rfloor n(n+1)$$

最后考虑$a<c$且$b<c$的情况。

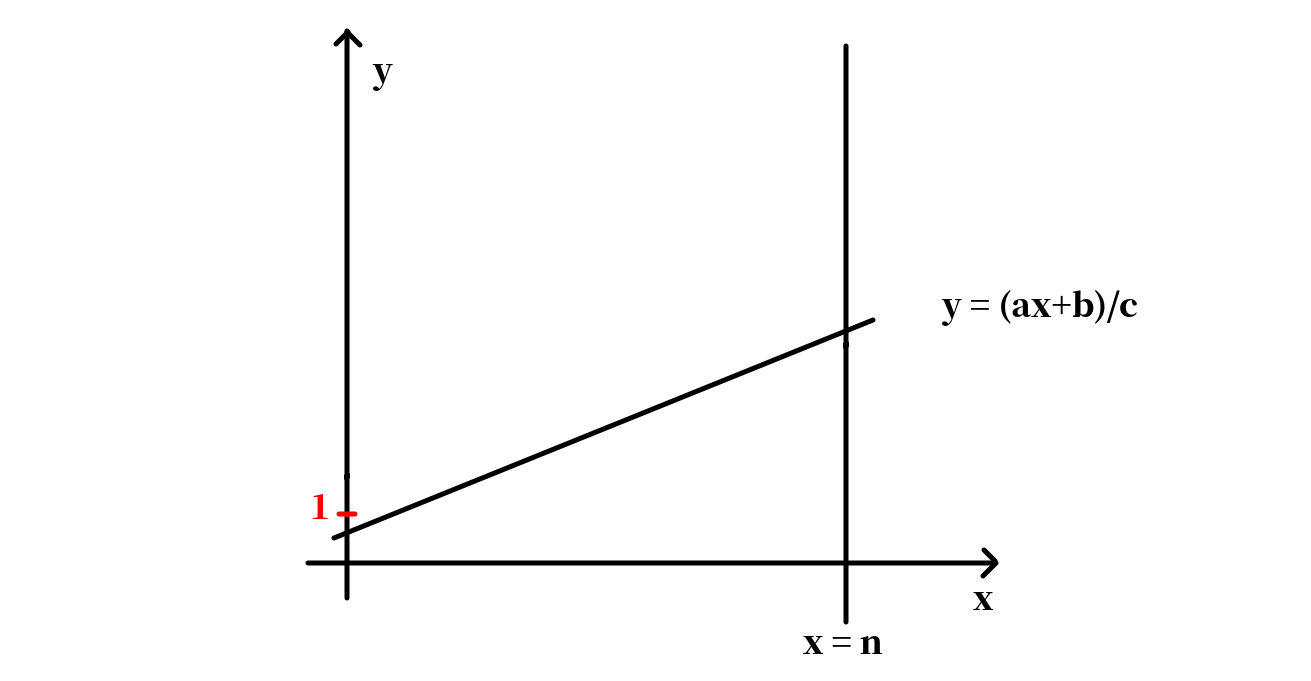
注意到在这种情况下，$l$与$y$轴的交点位于$[0, 1)$中。而直线的斜率小于$1$。这时我们考虑将平面沿$y=x$翻转：

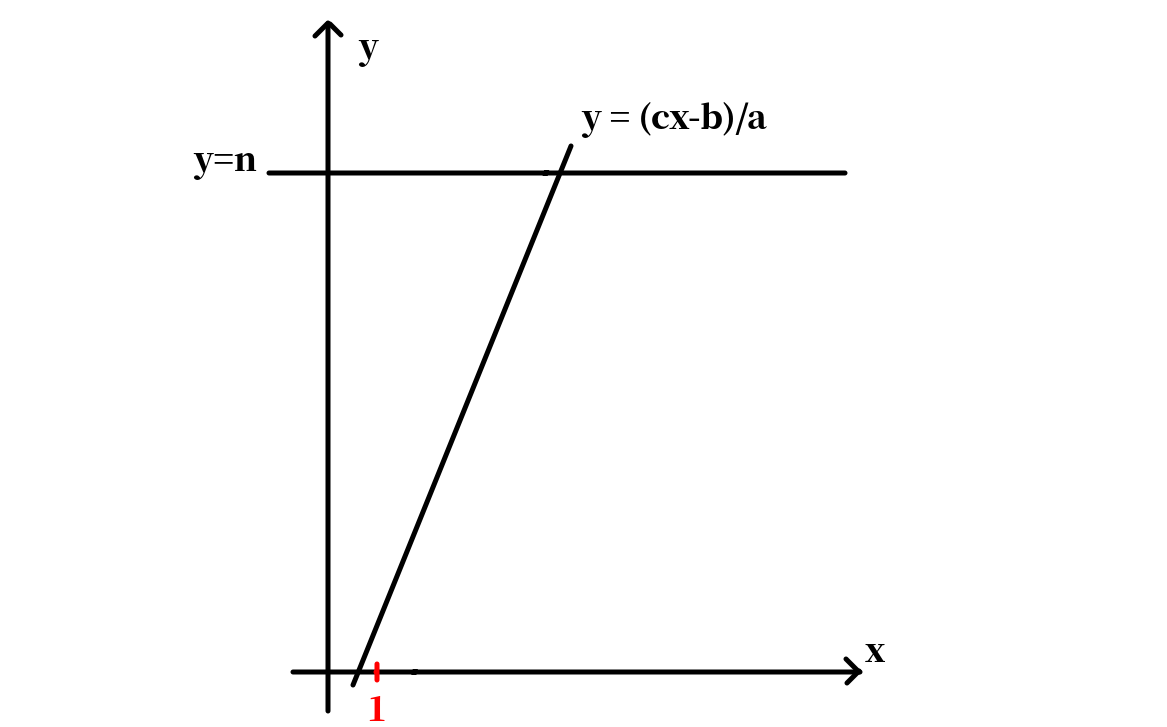
考虑用矩形的整点数减去三角形的整点数。不过这里引入了两个问题：

1. 求三角形的面积不属于我们定义的类欧问题，需要转化。
2. 求三角形的整点数时直线上的点是不能算的。

对于第一个问题很简单：把$y$轴向右平移一个单位即可。这样直线的解析式就变成$y = \frac{cx+c-b}{a}$。问题转化为矩形内整点数减去梯形内整点数。

对于第二个问题，我们将直线向下平移一点点即可。所谓的一点点指$\frac{1}{a}$。因此直线变成$y = \frac{cx+c-b-1}{a}$。

在翻转之后，$x$的上限取$\lfloor\frac{an+b}{c}\rfloor$。由于$y$轴向右平移了一个单位，因此实际上是$\lfloor\frac{an+b}{c}\rfloor-1$。

于是我们得到$f(a, b, c, n) = \lfloor\frac{an+b}{c}\rfloor n - f(c, c-b-1, a, \lfloor\frac{an+b}{c}\rfloor-1)$。

把三个转移合到一起就得到类欧几里德的完整算法了。

边界条件是$a=0$，此时$f(a, b, c, n) = \lfloor\frac{b}{c}\rfloor (n+1)$。

int f(int a, int b, int c, int n) {
  if(a == 0) {
    return (b/c)*(n+1);
  }
  if(a < c && b < c) {
    int m = (a*n+b)/c;
    return m*n - f(c, c-b-1, a, m-1);
  }
  return f(a%c, b%c, c, n) + (b/c)*(n+1) + (a/c)*(n*(n+1)/2);
}

问题扩展

考虑求$g(a, b, c, n) = \sum_{i=0}^n \lfloor \frac{ai+b}{c} \rfloor^2$，$h(a, b, c, n) = \sum_{i=0}^n i \lfloor \frac{ai+b}{c} \rfloor$。

对于$g$，可以理解为是给二维平面上的整点$(x,y)$定一个权值$w_g(x, y) = 2y-1$。那么我们要求的就是梯形里所有整点的点权和。

截矩形和截三角形的两种转移都可以容易地推出。问题在于沿$y=x$翻转后，此时的点权变成了$2x-1$，不太能用$g$描述子问题。

不妨看$h$。要求$h$，我们可以定点权$w_h(x, y) = x$。这时我们可以认为沿$y=x$翻转后，点权变成了$2w_h(x, y)-1$。也就是说我们可以用$h$和$f$描述$g$的转移。

同样的，对于$h$而言，前两种转移也是 trivial 的，而对于第三种转移，沿$y=x$翻转后点权变成了$y$，可以理解为是$\frac{1}{2}(w_h(x, y) + 1)$。因此我们同样可以用$g$和$f$描述$h$的转移。